Osnove kvantne mehanike

Preverjanje znanja

Izberi pravilni odgovor!

Katere od spodaj navedenih pojavov je mogoče popolnoma pojasniti samo z valovnimi lastnostmi svetlobe?
1. Mavrica.
2. Črtast absorbcijski spekter enoatomnih plinov.
3. Fotoefekt.
4. Sipanje rentgenskih žarkov na prostih elektronih.
5. Interferenca laserske svetlobe na uklonski mrežici.
6. Spekter sevanja črnega telesa.
7. Lom in odboj svetlobe na prehodu med dvema snovema.
8. Hitrost svetlobe v vakuumu.
Energija fotona pri elektromagnetnem (EM) valovanju je sorazmerna:
1. amplitudi EM valovanja.
2. frekvenci EM valovanja.
3. valovni dolžini EM valovanja.
4. hitrosti EM valovanja.
5. Energija fotona je neodvisna od valovnih lastnosti EM valovanja.
Na kovinsko ploščo posvetimo z enobarvno svetlobo. Od česa je odvisna maksimalna kinetična energija fotoelektronov, ki jih svetloba izbije iz plošče?
1. Od amplitude električnega polja v vpadnem EM valu.
2. Od frekvence svetlobe.
3. Od gostote svetlobnega toka.
4. Od časa obsevanja.
5. Od izstopnega dela kovine, iz katere je plošča.
Kolikšna je energija fotona vidne svetlobe (rdeče) z valovno dolžino 620 nm? (Produkt Planckove konstante (h = 6.626*10^(-34) Js) in hitrosti svetlobe (c=3.0*10^8 m/s) lahko zapišemo v bolj praktičnih enotah hc = 1242 eVnm)
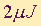
2. 2 eV
3. 620 eV
4. 770 keV
5. 2 J
Curek rdeče svetlobe z valovno dolžino 600 nm in curek modre svetlobe z valovno dolžino 450 nm padata na zaslon. Gostota energijskega toka je pri obeh curkih enaka. Pri katerem curku pade na zaslon več fotonov v enakem času?
1. Število fotonov na časovno enoto je enako pri obeh curkih.
2. Več fotonov na časovno enoto pade na zaslon pri modri svetlobi.
3. Več fotonov na časovno enoto pade na zaslon pri rdeči svetlobi.
Če posvetimo z laserskim žarkom na uklonsko mrežico, dobimo na zaslonu za mrežico značilno uklonsko sliko (uklonske maksimume). Kaj pa, če jakost laserskega žarka tako zmanjšamo, da na zaslon skozi mrežico prileti na enkrat le po en foton, če torej čez uklonsko mrežico spuščamo posamične fotone? Ali se bo po dovolj dolgem času, ko bomo na zaslonu detektirali dovolj fotonov, tudi pojavila enaka uklonska slika?
1. Uklonske slike ne dobimo, ker foton ne more interferirati sam s sabo na poti skozi uklonsko mrežico.
2. Uklonska slika bo na koncu enaka kot pri poskusu z močnim curkom.
3. Slika ne zaslonu ne bo pokazala značilnih interfernčnih masimumov, ampak bo enaka vsoti uklonskih slik, ki jih dobimo pri prehodu svetlobe skozi posamično režo.
4. Na zaslonu dobimo senco uklonske mrežice.
Pri kateri od spodaj navedenih elektromagnetnih valovanj imajo fotoni največjo gibalno količino?
1. Vidna svetloba
2. Radijski valovi
3. Rentgenski žarki
4. UV svetloba
Pri Comptonovem sipanju elektromagnetnega valovanja na prostih elektronih je valovna dolžina sipane svetlobe
1. enaka valovni dolžini vpadne svetlobe.
2. manjša od valovne dolžine vpadne svetlobe.
3. večja od valovne dolžine vpadne svetlobe.
4. odvisna od sipalnega kota sipane svetlobe glede na smer vpadne svetlobe.
Sipanje elektromagnetnega valovanja na prostih elektronih (Comptonovo sipanje) lahko pojasnimo samo če:
1. pojav opišemo kot elastični trk dveh delcev (fotona in elektrona), pri čemer moramo upoštevati ohranitev celotne gibalne količine in kinetične energije obeh delcev.
2. upoštevamo, da električno polje vpadnega elektromagnetnega valovanja, ki niha s frekvenco 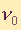, vzbudi nihanje elektrona, ki nato izseva elektromagnetno valovanje kot dipolna antena.
3. upoštevamo, da pride do uklona elektromagnetnega valovanja na elektronu.
Kateri pojav oziroma eksperiment dokazuje valovno naravo elektrona?
1. Fotoefekt.
2. Comptonov efekt.
3. Sipanje curka elektronov na kristalih.
4. Detekcija elektronov z elektronskim detektorjem.
Kaj se zgodi, če usmerimo ozek curek elektronov, ki imajo vsi enako kinetično energijo 50 eV, skozi tanek kovinski listič proti fluorescenčnemu zaslonu? Kovinski listič ima kristalno strukturo.
1. Elektroni se bodo na kristalni površini odbijali kot elastične žogice na gladki podlagi. Na zaslonu dobimo ves sipani curek na enem mestu (eno svetlo piko).
2. Elektroni se bodo sipali na kristalnih ravninah in interferirali med sabo kot enobarvna svetloba na uklonski mrežici. Na zaslonu dobimo uklonske maksimume (več razmaknjenih svetlih prog - koncentričnih obročev.).
3. Elektroni se bodo naključno sipali v vse smeri zaradi naključnih trkov s posameznimi atomi. Cel zaslon bo enakomerno osvetljen.
S katero količino je neposredno povezana valovna dolžina elektrona?
1. Z maso elektrona
2. Z gibalno količino elektrona
3. Z električnim nabojem elektrona
4. S spinom elektrona.
5. Z električno potencialno energijo elektrona.
De Broglieva valovna dolžina za elektron, ki se giblje s hitrostjo 1*10^5 m/s, je 7.3 nm. Kolikšna je valovna dolžina elektrona, ki se giblje dvakrat hitreje?
1. Enaka (7.3 nm): valovna dolžina elektrona ni odvisna od njegove hitrosti.
2. Dvakrat večja (14.6 nm)
3. Dvakrat manjša (3.65 nm)
4. Štirikrat večja (29.2 nm)
5. Štirikrat manjša (1.8 nm)
Oceni, kako natančno lahko določimo gibalno količino elektrona, ki je ujet v enodimenzionalni potencialni jami širine 0.1 nm. (Planckova konstanta: h = 6.626*10^(-34) Js)
1. Gibalno količino elektrona lahko ocenimo poljubno natančno.
2. Nenatančnost je večja od 6.6*10^(-24) kgm/s
3. Nenatančnost je večja od 0.5*10^(-24) kgm/s
4. Nenatančnost je manjša od 3.3*10^(-24) kgm/s
5. Gibalne količine elektrona sploh ne moremo določiti.
Elektron je ujet v potencialni jami s širino 10 nm. Ali lahko v taki potencialni jami miruje?
1. Vedno lahko miruje.
2. Lahko miruje samo pri dovolj nizki temperaturi okolice.
3. Lahko bi miroval samo pri absolutni ničli.
4. V nobenem primeru ne more mirovati. (To nam pove Heisenbergovo načelo nedoločenosti.)
Katera od spodnjih trditev je pravilna pri opisu elektrona, ki se, klasično gledano, elastično odbija med dvema stenama, ki sta razmaknjeni za razdaljo L?
1. Kinetična energija elektrona v osnovnem stanju je nič.
2. Elektron ima lahko poljubno kinetično energijo.
3. Gibalna količina elektrona je kvantizirana.
4. Gibalna količina elektrona je obratno sorazmerna z razdaljo med stenama L.
Valovno funkcijo elektrona označimo z 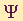. Kaj predstavlja ?
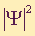1. Energijo
2. Gostoto energije
3. Verjetnost
4. Verjetnostno gostoto
Valovna funkcija elektrona, ki se giblje v enodimenzionalni potencialni jami s širino L, je normirana na naslednji način 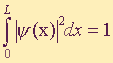. Kaj to pomeni?
1. Amplituda valovne funkcije je ena.
2. Valovna dolžina elektrona je ena.
3. Elektron se zagotovo nahaja znotraj potencialne jame.
4. Verjetnost, da najdemo elektron nekje znotraj potencialne jame, je ena.
5. Verjetnost, da najdemo elektron v ozkem intervalu širine dx je ena.
Elektron je ujet v enodimenzionalni potencialni jami z neskončno visokimi stenami, razmaknjenimi za razdaljo L. Katere od spodnjih trditev so pravilne.
1. Valovna funkcija elektrona v osnovnem stanju je podana z:
2. Energija elektrona v tretjem vzbujenem stanju je trikrat večja kot v osnovnem.
3. Ko je elektron v prvem vzbujenem stanju, je verjetnost, da ga najdemo na ozkem intervalu okoli sredine potencialne jame enaka nič. (Verjetnostna gostota ima vozel v sredini potencialne jame.)
Kateri od spodaj navedenih makroskopskih dogodkov bi lahko po analogiji ustrezal tunelskemu pojavu, ki ga poznamo pri osnovnih delcih?
1. Potovanje avtomobila iz ene strani hriba na drugo skozi tunel v hribu.
2. Prehod topovske granate skozi list papirja.
3. Naskakovanje svetovnega rekorda pri skokih v višino s palico. Po dovolj velikem številu poskusov tekmovalcu vendarle uspe preskočiti rekordno višino.
4. Kroglica v skledi v obliki polkrogle se kotali iz ene strani sklede na drugo (niha), tako da ne doseže zgornjega roba sklede, ampak se pri vsakem nihaju zaustavi nekaj centimetrov pod robom in se zakotali nazaj proti dnu. Ko nekaj časa tako potuje sem in tja po skledi, se nenadoma znajde na mizi zunaj sklede (brez naše pomoči).
Ko elektron tunelira skozi potencialno plast, je znotraj plasti:
1. kinetičn energija elektrona negativna.
2. hitrost elektrona negativna.
3. gibalna količina elektrona negativna.
4. masa elektrona negativna.
5. naboj elektrona pozitiven.
6. vrtilna količina elektrona negativna.