 |
 |
|||||||||||
| MPE | ||||||
| Večelektonske fotoeksitacije v atomu |
||||||
| Globoke dvojne fotoeksitacije v atomih (Ge..Rb) |
||||||
| Atomsko absorpcijsko ozadje |
||||||
TEORETIČNA SLIKA
Lastne energije in valovne funkcije atoma
Elektroni v atomu se gibljejo v privlačnem polju jedra in pri tem med sabo interagirajo z odbojno coulombsko silo. Nerelativistični hamiltonian za atom z N elektroni zapišemo kot vsoto enodelčnih in dvodelčnih operatorjev.
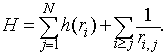 |
(1) |
Hamiltonian je zapisan v atomskih enotah. S h(r![]() ) smo označili nerelativistični enodelčni hamiltonian za gibanje i -tega elektrona v potencialu jedra z nabojem Z na razdalji r
) smo označili nerelativistični enodelčni hamiltonian za gibanje i -tega elektrona v potencialu jedra z nabojem Z na razdalji r![]()
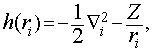 |
(2)) |
Drugi člen v (1) predstavlja odboj med elektroni. Dvojna vsota gre po vseh parih elektronov (i,j), pri čemer je ![]() razdalja obeh elektronov v paru.
razdalja obeh elektronov v paru.
Rešitev ![]() enačbe
enačbe
(3)) |
so valovne funkcije ![]() in lastne energije
in lastne energije ![]() za stacionarna stanja atoma. Točne rešitve
za stacionarna stanja atoma. Točne rešitve ![]() enačbe za atome z več elektroni ne moremo poznati zaradi fizičnih omejitev, zato je uporaba približkov neizbežna. Opis korelacij v gibanju elektronov
enačbe za atome z več elektroni ne moremo poznati zaradi fizičnih omejitev, zato je uporaba približkov neizbežna. Opis korelacij v gibanju elektronov
terja rešitve z valovnimi funkcijami, ki eksplicitno vsebujejo medelektronske razdalje ![]() . S takimi valovnimi funkcijami postane sistem preveč zapleten že pri N = 3 ali 4.
. S takimi valovnimi funkcijami postane sistem preveč zapleten že pri N = 3 ali 4.
Naloga se bistveno poenostavi, če nadomestimo točne medelektronske sile s povprečnimi, torej predpostavimo, da se vsak elektron giblje neodvisno od drugih v povprečnem centralno simetričnem polju jedra in preostalih N-1 elektronov. Zaradi simetrije se kotni del rešitve izdvoji, tako da valovno funkcijo elektrona (spin-orbitalo) zapišemo kot produkt radialnega, kotnega in spinskega dela
(4)) |
kjer imajo kvantna števila n, l, m![]() in m
in m![]() tak pomen, kot v primeru vodikovega atoma. Valovno funkcijo celotnega sistema N elektronov s pravilno permutacijsko simetrijo sestavimo v modelu centralno simetričnega polja iz enoelektronskih valovnih funkcij (4) v obliki antisimetriziranega produkta, ki ga zapišemo s Slaterjevo determinanto
tak pomen, kot v primeru vodikovega atoma. Valovno funkcijo celotnega sistema N elektronov s pravilno permutacijsko simetrijo sestavimo v modelu centralno simetričnega polja iz enoelektronskih valovnih funkcij (4) v obliki antisimetriziranega produkta, ki ga zapišemo s Slaterjevo determinanto
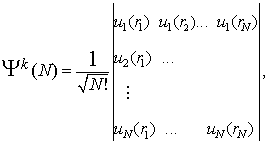 |
(5)) |
kjer označuje k izbrano konfiguracijo enoelektronskih spin-orbital.
Radialne dele spin-orbital je mogoče poiskati z variacijskim računom. Zahteva, da mora biti energijski funkcional
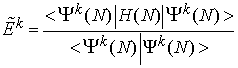 |
(6)) |
stacionaren na variacije radialnih funkcij P![]() (r) in da so spin-orbitale ortonormirane, vodi do Hartree-Fockovih enačb. To je sistem sklopljenih diferencialnih enačb, ki jih je mogoče reševati numerično z metodo samousklajenega polja [26,27].
(r) in da so spin-orbitale ortonormirane, vodi do Hartree-Fockovih enačb. To je sistem sklopljenih diferencialnih enačb, ki jih je mogoče reševati numerično z metodo samousklajenega polja [26,27].
Rešitev Hartree-Fockovih enačb pripelje do enodelčnih valovnih funkcij in lastne energije sistema za dano konfiguracijo k. Zaradi uporabe približka centralno simetričnega polja so korelacije med legami različnih elektronov zanemarjene. Z vpeljavo antisimetričnih valovnih fukcij (5), ki zadoščajo Paulijevemu izključitvenemu načelu, je izpolnjena zahteva, da dva elektrona s paralelnima spinoma ne moreta zasedati iste orbitale. Nobenih korelacij pa z antisimetričnimi valovnimi funkcijami ne vpeljemo med elektronoma z nasprotnima spinoma.
Valovne funkcije ![]() tvorijo poln sistem in lahko služijo kot baza za razvoj točnejših rešitev:
tvorijo poln sistem in lahko služijo kot baza za razvoj točnejših rešitev:
(7)) |
Pri tem zahtevamo, da je energijski funkcional stacionaren glede na variacije radialnih funkcij in mešalnih koeficientov C![]() . Sistem Hartree-Fockovih enačb je v tem primeru sklopljen s sekularnimi enačbami za mešalne koeficiente [26].
. Sistem Hartree-Fockovih enačb je v tem primeru sklopljen s sekularnimi enačbami za mešalne koeficiente [26].
Presek za fotoionizacijo
Uveljavljeni računski postopki za fotoabsorpcijski presek uporabljajo različne stopnje aproksimacije valovnih funkcij. Odnos med njimi si bomo ogledali na primeru preseka za fotoionizacijo. Interakcijo elektromagnetnega valovanja z elektroni v atomu obravnavamo kot šibko motnjo
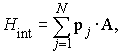 |
(8)) |
kjer je A operator vektorskega potenciala, p pa operator gibalne količine elektrona. Vsota teče po vseh N elektronih v atomu. Prehod atoma iz začetnega v končno stanje je podan že v prvem redu teorije motenj. Presek za fotoionizacijo je v dipolni aproksimaciji podan z
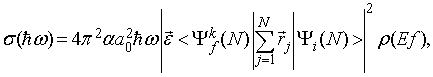 |
(9)) |
kjer je ![]() energija vpadnih fotonov,
energija vpadnih fotonov, ![]() polarizacijski vektor,
polarizacijski vektor, ![]() konstanta fine strukture,
konstanta fine strukture, ![]() Bohrov radij in
Bohrov radij in ![]() gostota končnih stanj.
gostota končnih stanj.
Začetno stanje opišemo s Slaterjevo determinato
(10)) |
Oznako za konfiguracijo izpustimo, ker je enolično določena z najnižjo energijo. Končno stanje opisuje fotoelektron v kontinuumu in ion v osnovni ali dodatni vzbuditvi. Končno valovno funkcijo izrazimo s Slaterjevo determinanto, ki jo sestavljajo vezane enoelektronske funkcije v![]() iona z vrzeljo v l-ti spin-orbitali ter valovna funkcija prostega fotoelektrona
iona z vrzeljo v l-ti spin-orbitali ter valovna funkcija prostega fotoelektrona ![]()
(11)) |
Indeks k označuje konfiguracijo iona. Ion v osnovni vzbuditvi opiše konfiguracija, pri kateri je zasedenih prvih N po energiji najnižjih spin-orbital, pri čemer je orbitala v![]() prosta. Označimo jo s k=0. Ko je po fotoionizaciji ion v stanju
prosta. Označimo jo s k=0. Ko je po fotoionizaciji ion v stanju ![]() , govorimo o enoelektronskem prehodu. O večelektronskih prehodih pa govorimo, ko je ion po prehodu v katerem od dodatno vzbujenih stanj
, govorimo o enoelektronskem prehodu. O večelektronskih prehodih pa govorimo, ko je ion po prehodu v katerem od dodatno vzbujenih stanj ![]() vključno z možnostjo dodatne ionizacije. Enoelektronske in večelektronske prehode računamo torej enako. Tip prehoda določa izbira končnega stanja
vključno z možnostjo dodatne ionizacije. Enoelektronske in večelektronske prehode računamo torej enako. Tip prehoda določa izbira končnega stanja ![]() .
.
Valovni funkciji začetnega in končnega stanja, ![]() in
in ![]() , sta rešitvi dveh različnih modelskih hamiltonianov, zato enoelektronske valovne funkcije, ki sestavljajo determinanto začetnega in končnega stanja, niso ortogonalne. Matrični element za dipolni prehod med dvema neortogonalnima Slaterjevima determinantama se izraža kot vsota enodelčnih dipolnih matričnih elementov, pomnoženih z monopolnimi prekrivanji ostalih enoelektronskih stanj
, sta rešitvi dveh različnih modelskih hamiltonianov, zato enoelektronske valovne funkcije, ki sestavljajo determinanto začetnega in končnega stanja, niso ortogonalne. Matrični element za dipolni prehod med dvema neortogonalnima Slaterjevima determinantama se izraža kot vsota enodelčnih dipolnih matričnih elementov, pomnoženih z monopolnimi prekrivanji ostalih enoelektronskih stanj
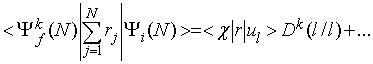 |
(12)) |
Izpisan je samo vodilni člen vsote, ki predstavlja dipolni prehod elektrona iz izbrane l-te spin-orbitale v kontinuum ter monopolno reorganizacijo ostalih elektronov v nova stanja iona. Vektorsko pisavo smo zaradi preglednosti opustili, ker nas odvisnosti preseka od polarizacije ne zanimajo. Determinanta ![]() označuje prekrivanje med poddeterminanto Slaterjeve determinante začetnega stanja brez l-te vrstice in l-tega stolpca
označuje prekrivanje med poddeterminanto Slaterjeve determinante začetnega stanja brez l-te vrstice in l-tega stolpca
(13)) |
in poddeterminanto Slaterjeve determinante končnega stanja brez valovne funkcije prostega elektrona ![]() , ki je kar Slaterjeva determinanta iona
, ki je kar Slaterjeva determinanta iona
(14)) |
Monopolno prekrivanje dveh Slaterjevih determinant se izraža kot determinanta enoelektronskih prekrivalnih integralov [28]
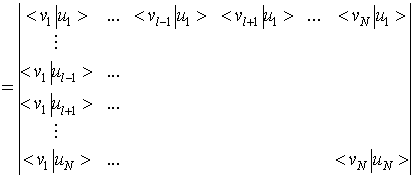 |
(15)) |
V razvoju matričnega elementa [12] so izpuščeni členi, ki opisujejo dipolni prehod enega od elektronov iz preostalih spin-orbital v kontinuum, končno stanje iona pa se vzpostavi preko monopolne relaksacije. Izpuščeni so tudi členi za monopolni prehod elektrona v kontinuum in hkratno relaksacijo ostalih elektronov v ionsko stanje, pri čemer eden od ostalih elektronov preide v končno stanje dipolno, ostali pa monopolno.
Vrednost prekrivalne determinante ![]() je vedno manjša od ena, vendar je za enoelektronske prehode blizu te vrednosti, ker so vsi diagonalni enolektronski prekrivalni integrali skoraj enaki ena zaradi podobnosti med funkcijami u
je vedno manjša od ena, vendar je za enoelektronske prehode blizu te vrednosti, ker so vsi diagonalni enolektronski prekrivalni integrali skoraj enaki ena zaradi podobnosti med funkcijami u![]() in v
in v![]() . Pri dvo- ali večelektronskih prehodih pa je njena vrednost bistveno manjša, ker se v končnem stanju vsaj en elektron nahaja v enem od vzbujenih stanj v
. Pri dvo- ali večelektronskih prehodih pa je njena vrednost bistveno manjša, ker se v končnem stanju vsaj en elektron nahaja v enem od vzbujenih stanj v![]() , ki se z začetnimi enoelektronskimi stanji u
, ki se z začetnimi enoelektronskimi stanji u![]() ne prekrivajo znatno. Od tod je tudi presek za dvo- ali večelektronski prehod bistveno manjši od preseka za enoelektronski prehod.
ne prekrivajo znatno. Od tod je tudi presek za dvo- ali večelektronski prehod bistveno manjši od preseka za enoelektronski prehod.
V poenostavljeni oceni enoelektronskega preseka (12) obdržimo le vodilni člen ter predpostavimo, da je prekrivalna determinanta ![]() enaka ena, ali drugače, da se enoelektronske spin-orbitale preostalih N-1 elektronov po fotoefektu ne relaksirajo (v
enaka ena, ali drugače, da se enoelektronske spin-orbitale preostalih N-1 elektronov po fotoefektu ne relaksirajo (v![]() =u
=u![]() ). To pomeni, da fotoionizacijo obravnavamo kot popolnoma enodelčni proces, pri katerem so preostali elektroni pasivni in ne občutijo nobene spremembe ob odstranitvi enega elektrona iz atoma. To je tako imenovani približek zamrznjene sredice, ki je zelo pogosto v uporabi pri računanju preseka za fotoefekt na širokem energijskem intervalu [3, 29]. Presek v približku zamrznjene sredice imenujemo tudi nerelaksirani enoelektronski presek. Preseku brez omenjenih približkov zamrznjene sredice pa zaradi razlikovanja rečemo relaksirani enoelektronski presek.
). To pomeni, da fotoionizacijo obravnavamo kot popolnoma enodelčni proces, pri katerem so preostali elektroni pasivni in ne občutijo nobene spremembe ob odstranitvi enega elektrona iz atoma. To je tako imenovani približek zamrznjene sredice, ki je zelo pogosto v uporabi pri računanju preseka za fotoefekt na širokem energijskem intervalu [3, 29]. Presek v približku zamrznjene sredice imenujemo tudi nerelaksirani enoelektronski presek. Preseku brez omenjenih približkov zamrznjene sredice pa zaradi razlikovanja rečemo relaksirani enoelektronski presek.
Približek nenadnega prehoda
V visokoenergijski limiti, daleč nad energijo praga, ima fotoelektron veliko kinetično energijo. Predpostavimo lahko, da po fotoefektu v trenutku zapusti atom in ne interagira z drugimi elektroni. Preostali elektroni občutijo le nenaden nastanek vrzeli v notranji podlupini, kar predstavlja trenutno motnjo, ki elektrone strese iz začetnega stanja nevtralnega atoma v lastna stanja iona. V tej limiti je mogoče pokazati [30], da nerelaksirani enoelektronski presek implicitno vsebuje enoelektronske in večelektronske prehode.
Razvijmo poddeterminanto Slaterjeve determinante začetnega stanja ![]() (13) po polni ortonormirani bazi končnih stanj iona
(13) po polni ortonormirani bazi končnih stanj iona ![]()
(16)) |
in upoštevajmo, da je ![]() normirana
normirana
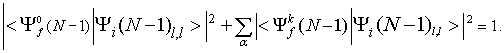 |
(17)) |
Nerelaksirani presek za fotoefekt je sorazmeren s kvadratom enoelektronskega matričnega elementa
(18)) |
Ko ga pomnožimo z gornjo identiteto (17)
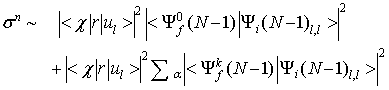 |
(19)) |
lahko razberemo, da je sestavljen iz dveh prispevkov
(20)) |
Prvi, ![]() , ustreza relaksiranemu enoelektronskemu preseku, drugi,
, ustreza relaksiranemu enoelektronskemu preseku, drugi, ![]() , pa preseku za večelektronske prehode. Pri tem smo predpostavili, da posamezni razpadni kanali v končnem stanju niso sklopljeni med sabo ter da so izpuščeni členi v razvoju matričnega elementa (12) zanemarljivo majhni. Nerelaksirani enoelektronski presek je torej vsota presekov za eno in večelektronske prehode. To pojasnjuje, zakaj se nerelaksirani enoelektronski presek za fotoabsorpcijo dobro ujema z izmerjenim polnim presekom pri energijah daleč nad absorpcijskimi robovi [3].
, pa preseku za večelektronske prehode. Pri tem smo predpostavili, da posamezni razpadni kanali v končnem stanju niso sklopljeni med sabo ter da so izpuščeni členi v razvoju matričnega elementa (12) zanemarljivo majhni. Nerelaksirani enoelektronski presek je torej vsota presekov za eno in večelektronske prehode. To pojasnjuje, zakaj se nerelaksirani enoelektronski presek za fotoabsorpcijo dobro ujema z izmerjenim polnim presekom pri energijah daleč nad absorpcijskimi robovi [3].
Iz izraza (19) je mogoče oceniti razmerje verjetnosti med eno- in večelektronskimi prehodi. Verjetnost za enoelektronski prehod je sorazmerna kvadratu prekrivalne determinante (15) ![]() . Spinski in kotni deli enoelektronskih spin-orbital u
. Spinski in kotni deli enoelektronskih spin-orbital u![]() in v
in v![]() so enaki. Zaradi monopolnih izbirnih pravil je mnogo izvendiagonalnih enoelektronskih prekrivalnih integralov v determinanti enako nič, preostali izvendiagonalni členi pa so majhni zaradi neznatnega prekrivanja med radialnimi deli enoelektronskih spin-orbital z različnimi glavnimi kvantnimi števili.
so enaki. Zaradi monopolnih izbirnih pravil je mnogo izvendiagonalnih enoelektronskih prekrivalnih integralov v determinanti enako nič, preostali izvendiagonalni členi pa so majhni zaradi neznatnega prekrivanja med radialnimi deli enoelektronskih spin-orbital z različnimi glavnimi kvantnimi števili.
Vrednost prekrivalne determinante ![]() tako določajo predvsem njeni diagonalni členi
tako določajo predvsem njeni diagonalni členi ![]() . če zanemarimo izvendiagonalne člene, preidemo v sliko neodvisnih delcev, v kateri lahko interpretiramo kvadrat enodelčnega prekrivalnega integrala
. če zanemarimo izvendiagonalne člene, preidemo v sliko neodvisnih delcev, v kateri lahko interpretiramo kvadrat enodelčnega prekrivalnega integrala ![]() kot verjetnost, da bo elektron, ki je v začetku v spin-orbitali i, ostal v isti spin-orbitali tudi po fotoionizaciji. Verjetnost, do bo i-to spin-orbitalo zapustil, je torej podana z
kot verjetnost, da bo elektron, ki je v začetku v spin-orbitali i, ostal v isti spin-orbitali tudi po fotoionizaciji. Verjetnost, do bo i-to spin-orbitalo zapustil, je torej podana z ![]() . Od tod lahko definiramo relativno verjetnost za hkratno ekscitacijo elektrona iz spin-orbitale u
. Od tod lahko definiramo relativno verjetnost za hkratno ekscitacijo elektrona iz spin-orbitale u![]() ob tvorbi vrzeli v l-ti spin-orbitali:
ob tvorbi vrzeli v l-ti spin-orbitali:
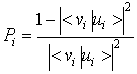 |
(21)) |
Izraz (21) se ujema z napovedmi modela za fotoionizacijo v približku nenadnega prehoda, ki ga je razvil Ǻberg [12]. Zaradi enostavnosti ga pogosto uporabljajo za oceno verjetnosti za večkratno fotoekscitacijo na atomih. Za žlahtne pline sta ustrezne verjetnosti za posamezne podlupine v odvisnosti od lege primarne vrzeli tabelirala Carlson in Krause [31], pri čemer sta v izrazu (21) upoštevala še popravke zaradi prepovedanih prehodov v že zasedena stanja.
Razmerje presekov za večelektronske in enoelektronske prehode je v približku nenadnega prehoda neodvisno od energije fotona (21). Primerjava z eksperimentalnimi rezultati [2, 32, 33, 34] potrjuje teoretične napovedi.
RAČUNANJE ENERGIJ ATOMSKIH NIVOJEV
Program GRASP
Programski paket GRASP [35, 36] omogoča računanje lastnih energij in valovnih funkcij atoma za izbrane elektronske konfiguracije. Elektrone v atomu obravnava relativistično. Postopek je analogen nerelativističnemu primeru, le računsko je zahtevnejši. Jedro programa je numerična integracija sistema sklopljenih Diracovih enačb za posamezne elektrone v povprečnem polju ostalih elektronov in končno razsežnega jedra. Program rešuje sistem enačb iterativno z metodo samousklajenega polja. V splošnem omogoča opis atomske valovne funkcije z mešanico konfiguracij. Poleg enoelektronskih valovnih funkcij, iz katerih je sestavljena N-elektronska valovna funkcija, izračuna program tudi mešalne koeficiente, za katere ima izbrana linearna kombinacija Slaterjevih determinant najnižjo energijo. Proceduro običajno označujejo s kratico MCDF -- Multiconfiguration Dirac-Fock [37, 38, 39].
K tako dobljeni lastni energiji izračuna program perturbativno tudi dva vodilna popravka kvantne elektrodinamike. Prvi upošteva lastno energijo elektrona, drugi pa je popravek zaradi polarizacije vakuma [40].
Natančnost izračunanih energij lahko preverimo na primeru ionizacijskih energij za vsako od ksenonovih podlupin L, za katere obstajajo natančni eksperimentalni podatki. Ionizacijska energija je definirana z razliko med lastno energijo osnovnega stanja nevtralnega atoma in najnižjo lastno energijo iona z vrzeljo v ustrezni podlupini. V osnovnem stanju ksenona so vse lupine zaključene. Celotna vrtilna količina J je enaka nič, parnost pa pozitivna. Tako stanje dobro opiše že ena sama konfiguracija, v kateri so po vrsti zapolnjene enoelektronske orbitale z najnižjo energijo: Xe = 1s![]() 2s
2s![]() 2p
2p![]() 3s
3s![]() 3p
3p![]() 3d
3d![]() 4s
4s![]() 4p
4p![]() 4d
4d![]() 5s
5s![]() 5p
5p![]() . Energija te konfiguracije, izračunana s programom GRASP, je E = -202388.5 eV. Ionizacijske energije, ki jih program daje za vsako od podlupin L v približku ene konfiguracije, so podane v tabeli 1. Stanje vrzeli je označeno v oglatem oklepaju, konfiguracija preostalih elektronov v ionu pa je ista kot v osnovnem stanju.
. Energija te konfiguracije, izračunana s programom GRASP, je E = -202388.5 eV. Ionizacijske energije, ki jih program daje za vsako od podlupin L v približku ene konfiguracije, so podane v tabeli 1. Stanje vrzeli je označeno v oglatem oklepaju, konfiguracija preostalih elektronov v ionu pa je ista kot v osnovnem stanju.

Tabela 1: Ionizacijske energije (v eV) ksenonovih podlupin L. Energije, izračunane s programom GRASP, so podane v prvem stolpcu
(E![]() ). V drugem stolpcu so teoretične vrednosti (E
). V drugem stolpcu so teoretične vrednosti (E![]() -- many-body perturbation theory), pri katerih so upoštevani perturbativni popravki zaradi korelacij med elektroni [41]. Eksperimentalne vrednosti ionizacijskih energij so izmerjene s fotoelektronsko spektroskopijo (XPS -- X-ray Photoelectron Spectroscopy) [42] ter v absorpcijski tehniki (XAS -- X-ray Absorption Spectroscopy) [43].
-- many-body perturbation theory), pri katerih so upoštevani perturbativni popravki zaradi korelacij med elektroni [41]. Eksperimentalne vrednosti ionizacijskih energij so izmerjene s fotoelektronsko spektroskopijo (XPS -- X-ray Photoelectron Spectroscopy) [42] ter v absorpcijski tehniki (XAS -- X-ray Absorption Spectroscopy) [43].
Iz primerjave med izračunanimi vrednostimi (E![]() ) in eksperimentalnimi podatki je razvidno, da je ujemanje za podlupini 2p
) in eksperimentalnimi podatki je razvidno, da je ujemanje za podlupini 2p![]() in 2p
in 2p![]() natančno na 1 eV. Za podlupino 2s pa je razhajanje bistveno večje in znaša približno 6 eV. Tako razhajanje je posledica približkov pri računanju energij. V enokonfiguracijskem približku so pri variacijskem računu z metodo samovsklajenega polja zanemarjene korelacije med elektroni. Za primerjavo so v tabeli 1 podane tudi teoretične vrednosti za ionizacijske energije E
natančno na 1 eV. Za podlupino 2s pa je razhajanje bistveno večje in znaša približno 6 eV. Tako razhajanje je posledica približkov pri računanju energij. V enokonfiguracijskem približku so pri variacijskem računu z metodo samovsklajenega polja zanemarjene korelacije med elektroni. Za primerjavo so v tabeli 1 podane tudi teoretične vrednosti za ionizacijske energije E![]() , ki so dobljene v okviru relativistične mnogodelčne perturbativne teorije [41]. Z upoštevanjem perturbativnih popravkov zaradi korelacij med elektroni so avtorji dosegli ujemanje teoretičnih energij z eksperimentalnimi vrednostmi v okviru natančnosti meritev.
, ki so dobljene v okviru relativistične mnogodelčne perturbativne teorije [41]. Z upoštevanjem perturbativnih popravkov zaradi korelacij med elektroni so avtorji dosegli ujemanje teoretičnih energij z eksperimentalnimi vrednostmi v okviru natančnosti meritev.
Opis stanj pri dvoelektronskih prehodih
Kot smo že omenili, ločimo pri dvoelektronskih prehodih tri tipe: resonančne prehode, pri katerih oba elektrona preideta v prosta vezana stanja in atom ostane nevtralen, prehode ''shake-up'', pri katerih en od obeh elektronov preide v kontinuum ter prehode ''shake-off'', pri katerih preideta v kontinuum oba elektrona. Energija, pri kateri lahko posamezen prehod poteče, je podana z razliko med lastno energijo atoma oziroma iona v ustreznem končnem stanju in lastno energijo atoma v osnovnem stanju.
Izbira elektronskih konfiguracij za opis končnega stanja je najenostavnejša pri določanju praga za prehod ''shake-off''. Poiskati je potrebno konfiguracijo dvakrat ioniziranega atoma, ki ima pri danem paru vrzeli najnižjo lastno energijo. Med resonančnimi dvoelektronskimi prehodi so najverjetnejši tisti, pri kateri oba elektrona preideta v najnižja nezasedena vezana stanja. Pri tem mora biti zaradi izbirnih pravil izpolnjen pogoj, da je celotna vrtilna količina atoma v končnem stanju J=1. Take zahteve za končno stanje atoma po procesih ''shake-up'' in ''shake-off'' ni, ker del vrtilne količine odnese eden oziroma oba elektrona, ki preideta v kontinuum. Pri izbiri možnih končnih stanj za prehode ''shake-up'' se lahko opiramo le na kvalitativno oceno, da so najbolj verjetni tisti prehodi, pri katerih preide en elektron dipolno v kontinuum, drug pa monopolno v najnižje nezasedeno vezano stanje. Možni so sicer tudi prehodi ''shake-up'', pri katerih elektron monopolno preide v višja Rydbergova stanja, vendar so manj verjetni. Manj verjetni so tudi tako imenovani konjugirani prehodi ''shake-up'', pri katerih en elektron preide monopolno v kontinuum, drugi elektron pa dipolno v vezano stanje.
Po dvoelektronskih prehodih ima atom od dve do štiri odprte podlupine, kar pripelje do bogate multipletnosti končnih stanj. že v enokonfiguracijskem približku je število relativističnih N-elektronskih valovnih funkcij z enako parnostjo in celotno vrtilno količino pri izbrani porazdelitvi elektronov po podlupinah tipično nekaj deset, lahko pa jih je tudi preko sto. Stanja v multipletu se po energiji razlikujejo. Energijska širina multipleta je odvisna od konfiguracije. Z opisom končnega stanja z mešanico dveh ali več konfiguracij se ustrezno poveča tako število stanj v multipletu, kot tudi energijska širina multipleta.
Za ilustracijo si lahko ogledamo primer dvojnega resonančnega prehoda v ksenonu, pri katerem pride ob vzbuditvi podlupine L![]() do hkratne ekscitacije elektrona v podlupini 5p. Ena izmed možnih konfiguracij končnega stanja je [2s5p]6p
do hkratne ekscitacije elektrona v podlupini 5p. Ena izmed možnih konfiguracij končnega stanja je [2s5p]6p![]() , kjer sta v oklepaju označeni stanji vrzeli, ekscitirana elektrona pa sta v vzbujenih stanjih 6p. Za to konfiguracijo je možnih 14 relativističnih N-elektronskih valovnih funkcij z negativno parnostjo in celotno vrtilno količino J=1. Energijska širina multipleta je 3.0 eV, najnižja energija v multipletu pa 5471.4 eV. V primeru, ko končno stanje po prehodu opišemo z mešanico konfiguracij [2s5p]6p
, kjer sta v oklepaju označeni stanji vrzeli, ekscitirana elektrona pa sta v vzbujenih stanjih 6p. Za to konfiguracijo je možnih 14 relativističnih N-elektronskih valovnih funkcij z negativno parnostjo in celotno vrtilno količino J=1. Energijska širina multipleta je 3.0 eV, najnižja energija v multipletu pa 5471.4 eV. V primeru, ko končno stanje po prehodu opišemo z mešanico konfiguracij [2s5p]6p![]() in [2s5p]5d
in [2s5p]5d![]() , naraste število stanj v multipletu na 32, širina multipleta pa se poveča. Najnižja energija v multipletu je za 1.5 eV nižja kot v enokonfiguracijskem približku.
, naraste število stanj v multipletu na 32, širina multipleta pa se poveča. Najnižja energija v multipletu je za 1.5 eV nižja kot v enokonfiguracijskem približku.
Izračunane energije dvoelektronskih prehodov v ksenonu, povezanih s tvorbo vrzeli v podlupini L in eni od zunanjih lupin, ki jih v enokonfiguracijskem približku dobimo s programom GRASP, so vsaj tako nenatančne, kot na enak način izračunane ioni\-za\-cij\-ske energije podlupin L (Tabela 1). Vendar lahko predpostavimo, da so popravki zaradi korelacij med elektroni k izračunanim energijam dvoelektronskih prehodov nad posameznim robom L po velikosti približno enaki popravkom za ionizacijsko energijo na istem robu
(Tabela 1 E![]() - E
- E![]() . Namesto absolutnih energij dvoelektronskih prehodov zato raje uporabljamo relativne energije glede na ionizacijsko energijo ustrezne podlupine L, tako da se omenjeni popravki v vodilnem redu kompenzirajo. Relativne energije so nenatančne le še toliko, kolikor je pri računanju zanemarjen premik energijskih nivojev zaradi korelacij med elektroni v vzbujenih stanjih in zaradi korelacij ob nastanku vrzeli v zunanji lupini. Napako v relativni energiji lahko v grobem ocenimo iz primerjave med izračunanimi in izmerjenimi ionizacijskimi energijami za ksenonove zunanje podlupine [44]. Razhajanja so reda velikosti 1 eV. Podobno nenatančnost lahko pričakujemo tudi pri izračunanih relativnih energijah dvoelektronskih prehodov.
. Namesto absolutnih energij dvoelektronskih prehodov zato raje uporabljamo relativne energije glede na ionizacijsko energijo ustrezne podlupine L, tako da se omenjeni popravki v vodilnem redu kompenzirajo. Relativne energije so nenatančne le še toliko, kolikor je pri računanju zanemarjen premik energijskih nivojev zaradi korelacij med elektroni v vzbujenih stanjih in zaradi korelacij ob nastanku vrzeli v zunanji lupini. Napako v relativni energiji lahko v grobem ocenimo iz primerjave med izračunanimi in izmerjenimi ionizacijskimi energijami za ksenonove zunanje podlupine [44]. Razhajanja so reda velikosti 1 eV. Podobno nenatančnost lahko pričakujemo tudi pri izračunanih relativnih energijah dvoelektronskih prehodov.
Aproksimizacija Z+1
Zaradi težavnosti in nenatančnosti računanja energij dvoelektronskih prehodov si poskušamo pomagati z izmerjenimi energijami prehodov v analognem atomskem sistemu. Atomski potencial, ki ga občutijo elektroni v zunanjih lupinah, je pri atomu z vrstnim številom Z in vrzeljo v eni od notranjih lupin ekvivalenten tistemu v nevtralnem atomu z vrstnim številom Z+1 \cite{king}. Razpored zunanjih nivojev in energijske razlika med njimi so v obeh primerih približno enaki. Ksenonu z vrstnim stevilom Z=54 in vrzeljo v notranji lupini torej približno ustrezajo nivoji v Cs II (Z=55). Nevtralni cezij ima v osnovnem stanju zasedeno podlupino 6s, ki je pri ksenonu prosta. Zato je za primerjavo s ksenonom primernejši enkrat ionizirani cezij (Cs II) brez elektrona 6s.
Pri dvoelektronskih prehodih pride ob nastanku vrzeli v notranji podlupini še do prehoda enega od zunanjih elektronov. Relativne energije dvojnih prehodov glede na ionizacijsko energijo podlupine L ksenona lahko torej ocenimo z eksperimentalno določenimi energijami ustreznih optičnih prehodov v Cs II. Vrednosti, ki jih dobimo za relativne energije dvoelektronskih prehodov z aproksimacijo Z+1, se ujemajo z izračunanimi vrednostmi v okviru nekaj eV.
| |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||