 |
 |
|||||||||||
| MPE | ||||||
| Večelektonske fotoeksitacije v atomu |
||||||
| Globoke dvojne fotoeksitacije v atomih (Ge..Rb) |
||||||
| Atomsko absorpcijsko ozadje |
||||||
Xe ROBOVI
Eksperimentalna oprema
Meritve absorpcijskega koeficienta ksenona v okolici absorpcijskih robov L so bile opravljene na eksperimentalni postaji EXAFS II v laboratoriju HASYLAB, DESY. Postavitev eksperimenta je shematično prikazana na sliki 5. Vir svetlobe je sinhrotronsko sevanje iz
shranjevalnega obroča DORIS z energijo elektronov 5.3 GeV in maksimalnim tokom 40mA. Snop sinhrotronske svetlobe je s toroidnim zrcalom fokusiran na dvokristalni silicijev monokromator Si(111). Energijska ločljivost monokromatorja v območju 5 keV je 1 eV. Visoko stabilni monokromatorski pogon z vgrajeno povratno zanko skrbi, da je svetlobni tok monokromatizirane svetlobe med meritvijo konstanten.
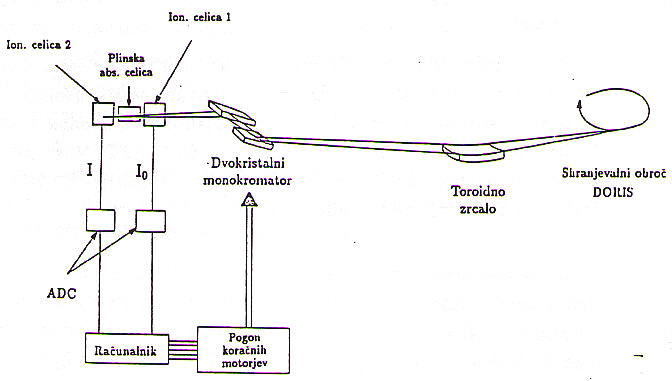
Slika 5: Shematični prikaz postavitve eksperimenta.
Sinhrotronska svetloba je speljana po vakuumu. V vakuumsko posodo je vgrajena 40 mm dolga plinska absorpcijska celica z oknoma
iz 0.5 mm debelega stekla pleksi. Intenziteto vpadnega in prepuščenega curka svetlobe, I![]() in I, merita ionizacijski celici, napolnjeni z
in I, merita ionizacijski celici, napolnjeni z
dušikom. Energijsko področje ksenonovih robov L je posneto v energijskih korakih od 0.2 eV do 1 eV. čas merjenja pri izbrani energiji vpadnega curka je 1s, vpadni svetlobni tok pa reda velikosti 10![]() fotonov/s.
fotonov/s.
Absorpcijska celica je priključena na sekundarni vakuumski sistem, ki omogoča praznjenje in kontrolirano polnjenje celice, ne da bi pri tem spremenili njeno lego glede na svetlobni snop. To zagotovlja ponovljivost meritev na absorberju in nespremenjene pogoje za referenčne meritve brez absorberja.
Rezultati meritev
Spektri absorpcije, ln{(I![]() /I), so izmerjeni na celici, napolnjeni s ksenonom s čistočo 99.995\% pri tlaku 12.0 kPa in pri temperaturi 24
/I), so izmerjeni na celici, napolnjeni s ksenonom s čistočo 99.995\% pri tlaku 12.0 kPa in pri temperaturi 24![]() C. Pri izbranem tlaku je za absorpcijsko celico dosežena optimalna absorpcijska debelina (
C. Pri izbranem tlaku je za absorpcijsko celico dosežena optimalna absorpcijska debelina (![]() ) za merjenje majhnih sprememb absorpcijskega koeficienta. K vsakemu absorpcijskemu spektru je posnet referenčni spekter pri prazni celici. Razlika obeh spektrov, v kateri je izločena absorpcija v oknih absorpcijske celice, kot tudi izkoristek obeh ionizacijskih celic, predstavlja absolutno izmerjeni spekter absorpcijske debeline
) za merjenje majhnih sprememb absorpcijskega koeficienta. K vsakemu absorpcijskemu spektru je posnet referenčni spekter pri prazni celici. Razlika obeh spektrov, v kateri je izločena absorpcija v oknih absorpcijske celice, kot tudi izkoristek obeh ionizacijskih celic, predstavlja absolutno izmerjeni spekter absorpcijske debeline ![]() vzorca. Iz nje lahko določimo atomski presek za fotoabsorpcijo v ksenonu
vzorca. Iz nje lahko določimo atomski presek za fotoabsorpcijo v ksenonu ![]() , kjer je N število atomov na volumsko enoto. Nenatančnost v absolutni skali preseka, ki je posledica nenatančnosti pri merjenju tlaka, temperature in dolžine celice, znaša
, kjer je N število atomov na volumsko enoto. Nenatančnost v absolutni skali preseka, ki je posledica nenatančnosti pri merjenju tlaka, temperature in dolžine celice, znaša ![]() 2%.
2%.
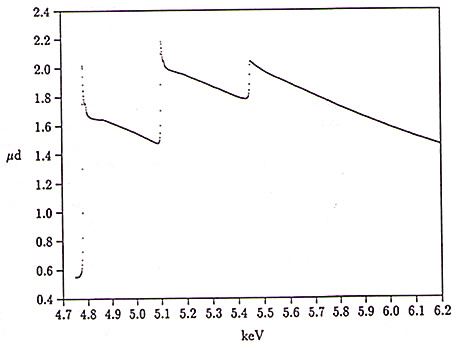
Slika 6: Spekter absorpcijske debeline ![]() ksenona v okolici absorpcijskih robov L.
ksenona v okolici absorpcijskih robov L.
Rezultat meritev je za energijsko območje, ki pokriva vse tri absorpcijske robove L, prikazan na sliki 6. Merjeni rob ne sovpada s pragom za fotoionizacijo, ker so predenj naloženi prispevki resonančnih prehodov 2s![]() np oziroma 2p
np oziroma 2p![]() nd. Kot smo videli, se vodilni prispevek te serije pri argonu pokaže kot močna črta pred robom (''white line''), pri robovih L ksenona pa je zaradi večje naravne širine (
nd. Kot smo videli, se vodilni prispevek te serije pri argonu pokaže kot močna črta pred robom (''white line''), pri robovih L ksenona pa je zaradi večje naravne širine (![]() = 3eV) opažen samo rahel dvig pri robovih L
= 3eV) opažen samo rahel dvig pri robovih L![]() in L
in L![]() (slike 7, 8 in 9). Zgradba roba, ki je potrebna za natančno energijsko kalibracijo, je povzeta po detajlni meritvi oblike robov [43]. S tem umerimo energijsko skalo na 0.5 eV.
(slike 7, 8 in 9). Zgradba roba, ki je potrebna za natančno energijsko kalibracijo, je povzeta po detajlni meritvi oblike robov [43]. S tem umerimo energijsko skalo na 0.5 eV.
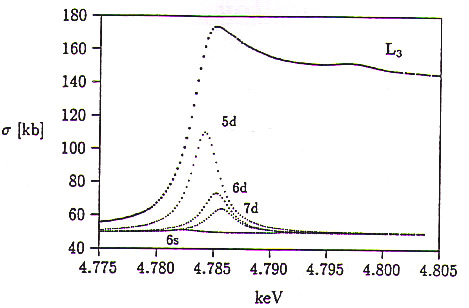
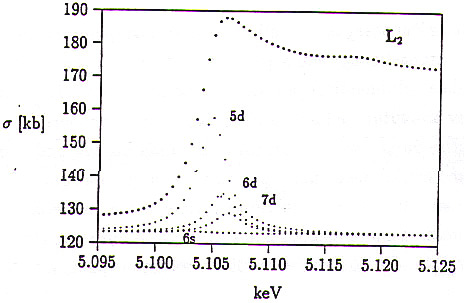
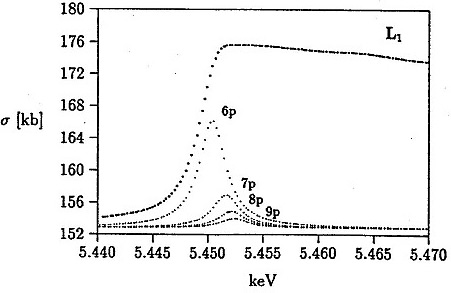
Slike 7, 8, 9: Povečan prikaz absorpcijskih robov L![]() , L
, L![]() in L
in L![]() . V slike je vrisan delež diskretnih prehodov pod pragom za fotoionizacijo po ref. [43].
. V slike je vrisan delež diskretnih prehodov pod pragom za fotoionizacijo po ref. [43].
ANALIZA MERITEV
O metodi analize
Informacija, ki jo je mogoče izluščiti iz izmerjenega absorpcijskega spektra, je omejena z eksperimentalno ločljivostjo in razmerjem signal-šum. V našem primeru je prva omejitev zanemarljiva: eksperimentalna ločljivost je manjša od naravne širine vzbujenih stanj, ki so vključena v proces fotoabsorpcije. Prispevkov različnih reakcijskih kanalov, ki se v spektru delno ali popolnoma zlivajo, torej v načelu ni mogoče razločiti z boljšo spektrometrijo -- gre za naravno mešanje in interferenco stanj.
Dinamični obseg izmerjenih vrednosti absorpcijske debeline znaša nekaj enot, amplituda stohastičnega šuma pa je ![]() . Učinki kolektivnih pojavov predstavljajo le majhen del dinamičnega obsega, zato so opazni šele po primerni povečavi. Ker je meritev absolutna, je idealna metoda povečave primerjava z modelskimi vrednostmi, s čimer se najučinkoviteje zmanjša dinamični obseg podatkov. Kot se pokaže, lahko najdemo kolektivne učinke v preseku vse do nivoja šuma. Potrebne so torej povečave v razponu 10
. Učinki kolektivnih pojavov predstavljajo le majhen del dinamičnega obsega, zato so opazni šele po primerni povečavi. Ker je meritev absolutna, je idealna metoda povečave primerjava z modelskimi vrednostmi, s čimer se najučinkoviteje zmanjša dinamični obseg podatkov. Kot se pokaže, lahko najdemo kolektivne učinke v preseku vse do nivoja šuma. Potrebne so torej povečave v razponu 10![]() , česar z eno samo primerjavo z modelskimi vrednostmi ne moremo premostiti. Tako je mogoče izluščiti najdrobnejše strukture le z ad-hoc funkcijskimi nastavki, torej z lokalnimi modeli izmerjenega spektra.
, česar z eno samo primerjavo z modelskimi vrednostmi ne moremo premostiti. Tako je mogoče izluščiti najdrobnejše strukture le z ad-hoc funkcijskimi nastavki, torej z lokalnimi modeli izmerjenega spektra.
Za razliko od globalnih teoretičnih modelov pa lokalni modeli neizogibno popačijo naravo drobnih struktur, ker izbrišejo njihove asimptotske poteke. Ta postopek ne prizadene edino resonančnih prispevkov k preseku, v drobnih absorpcijskih robovih ostane viden sam skok, medtem ko se informacija o zlomu pri procesih ''shake-off'' praktično izgubi. Zato se v interpretaciji drobnih struktur omejimo samo na prva dva tipa pojavov.
Primerjava meritev z modelom neodvisnih delcev
Primerjava izmerjenega preseka za fotoabsorpcijo v ksenonu z izračunanimi vrednostmi, dobljenimi v okviru dveh različnih enoelektronskih računov, je predstavljena na sliki 10. Oba računa izhajata iz približka zamrznjene sredice v relativističnem hamiltonianu. Sasakijeve vrednosti [29] so dobljene s poenostavljenimi valovnimi funkcijami, tako da je presek posamičnih podlupin podan s preprostim potenčnim izrazom E![]() , kjer ima konstanta
, kjer ima konstanta ![]() za podlupinske prispevke L
za podlupinske prispevke L![]() , L
, L![]() oziroma L
oziroma L![]() vrednosti 1.50, 2.03 oziroma 3.47, za prispevek ostalih lupin pa 2.61. Scofieldove vrednosti [3, 46] so dobljene v aproksimaciji Hartree-Slaterjevega potenciala [27] in pokažejo tudi odmike od potenčnega poteka v bližini robov.
vrednosti 1.50, 2.03 oziroma 3.47, za prispevek ostalih lupin pa 2.61. Scofieldove vrednosti [3, 46] so dobljene v aproksimaciji Hartree-Slaterjevega potenciala [27] in pokažejo tudi odmike od potenčnega poteka v bližini robov.
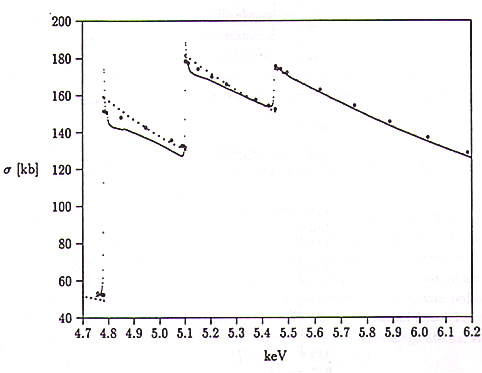
Slika 10: Primerjava izmerjenega preseka za fotoabsorpcijo z izračunanimi vrednostmi: (...) -- Meritve; (![]() ) -- Sasaki; (
) -- Sasaki; (![]() ) -- Scofield.
) -- Scofield.
V obeh primerih ugotovimo ujemanje z eksperimentalnimi vrednostmi v okviru natančnosti meritev na obeh skrajnih mejah obravnavanega energijskega območja. To je v skladu s teoretičnimi napovedmi [30], da nerelaksirani enoelektronski presek pri energijah daleč nad absorpcijskimi robovi ustreza polnemu, ne pa enoelektronskemu preseku za fotoionizacijo.
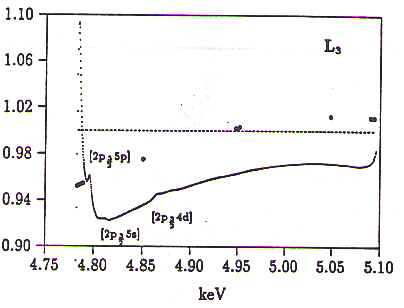
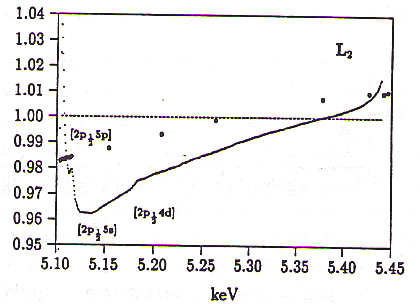
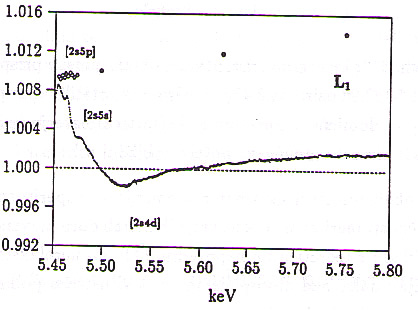
Slike 11, 12, 13: Odstopanje izmerjenega preseka od tabeliranega enoelektroskega preseka nad vsakim od robov L. Izmerjene vrednosti so deljene s teoretičnimi vrednostmi [29]. (...) -- Meritve; (- - -) -- Sasaki; (![]() ) -- Scofield. Označena so groba energijska območja možnih vzbuditev.
) -- Scofield. Označena so groba energijska območja možnih vzbuditev.
Nazornejšo predstavo o razhajanjih eksperimentalnih in teoretičnih vrednosti ponujajo slike 11, 12 in 13, kjer je podano razmerje obojih vrednosti za vsak rob L posebej. Za normalizacijo so uporabljene Sasakijeve vrednosti, ki omogočajo lažjo interpolacijo. Scofieldove vrednosti sicer kažejo boljše ujemanje z izmerjenimi, vendar pa so podane v relativno velikih energijski razmikih, kar otežuje interpolacijo med njimi.
Glede na dobro ujemanje teoretičnih in eksperimentalnih vrednosti nad robom L![]() dosežemo z opisanim postopkom zmanjšanje dinamičnega razpona za faktor 100 in temu ustrezno povečavo. Razen drobnih struktur, ki jih bomo podrobneje obdelali kasneje, opazimo razhajanje le v območju 70 eV tik nad robom.
dosežemo z opisanim postopkom zmanjšanje dinamičnega razpona za faktor 100 in temu ustrezno povečavo. Razen drobnih struktur, ki jih bomo podrobneje obdelali kasneje, opazimo razhajanje le v območju 70 eV tik nad robom.
Kot smo omenili že v uvodnih poglavjih, so povečani naklon nad robom opazili že nad vsemi robovi K žlahtnih plinov. Razlaga temelji na dejstvu, da fotoinizacija v bližini praga poteče počasi. Glavni vzrok za povečanje preseka v neposredni bližini roba je adiabatna prilagoditev elektronov na nov atomski potencial ob nastanku vrzeli v notranji lupini. Poleg tega lahko pride do razpada vrzeli z Augerjevim pojavom. Taka dodatna reorganizacija atomske sredice povzroči, da se počasni fotoelektron na poti iz atoma giblje v potencialu dvakrat namesto enkrat ioniziranega atoma, kar še dodatno prispeva k povečanju preseka neposredno nad robom.
Nad roboma L![]() in L
in L![]() se z normalizacijskim postopkom dinamični razpon zmanjša le za faktor 10. Pretežni del tega razpona napenja sama struktura roba z resonančnimi prehodi 2p
se z normalizacijskim postopkom dinamični razpon zmanjša le za faktor 10. Pretežni del tega razpona napenja sama struktura roba z resonančnimi prehodi 2p![]() nd (slike 7, 8, 9), katerih prispevki v Sasakijevem računu niso upoštevani. Eliminacija te črte tudi tu razkrije povečan naklon preseka nad robom, vendar je doseg tega učinka (20 eV) bistveno manjši kot pri L
nd (slike 7, 8, 9), katerih prispevki v Sasakijevem računu niso upoštevani. Eliminacija te črte tudi tu razkrije povečan naklon preseka nad robom, vendar je doseg tega učinka (20 eV) bistveno manjši kot pri L![]() in povzroči tudi ustrezno manjšo absolutno spremembo preseka.
in povzroči tudi ustrezno manjšo absolutno spremembo preseka.
Za razliko od robu L![]() opazimo nad L
opazimo nad L![]() in L
in L![]() razhajanje absolutnih eksperimentalnih in teoretičnih vrednosti prek meja eksperimentalne napake. V vsem območju med robovi se naklon energijskega poteka preseka razlikuje od teoretične napovedi. Podoben učinek je pri prehodnih težkih elementih od Hf do Pb opazil Jitschin [47] (slika 14). Razložil ga je z modelom dielektrične polarizacije podlupin 2p v polju vpadne svetlobe. Podobno kot pri Starkovem pojavu se elektronski oblak v zunanjem izmeničnem polju deformira. Spremenjeno senčenje spremeni presek za fotoabsorpcijo. Dielektrična polarizacija posameznih lupin je najbolj izrazita v okolici absorpcijskih robov. Zaradi korelacij med elektroni se deformacija ene lupine zrcali tudi na sosednjih lupinah, tako da se pri absorpcijskem robu ene lupine spremeni presek za fotoabsorpcijo tudi na ostalih.
razhajanje absolutnih eksperimentalnih in teoretičnih vrednosti prek meja eksperimentalne napake. V vsem območju med robovi se naklon energijskega poteka preseka razlikuje od teoretične napovedi. Podoben učinek je pri prehodnih težkih elementih od Hf do Pb opazil Jitschin [47] (slika 14). Razložil ga je z modelom dielektrične polarizacije podlupin 2p v polju vpadne svetlobe. Podobno kot pri Starkovem pojavu se elektronski oblak v zunanjem izmeničnem polju deformira. Spremenjeno senčenje spremeni presek za fotoabsorpcijo. Dielektrična polarizacija posameznih lupin je najbolj izrazita v okolici absorpcijskih robov. Zaradi korelacij med elektroni se deformacija ene lupine zrcali tudi na sosednjih lupinah, tako da se pri absorpcijskem robu ene lupine spremeni presek za fotoabsorpcijo tudi na ostalih.
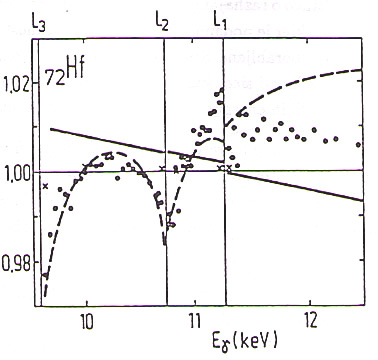
Slika 14: Primerjava med eksperimentalnim in teoretičnim presekom za fotoabsorpcijo v okolici absorpcijskih robov L hafnija [47] . (![]() ) eksperimentalne vrednosti; (---) model neodvisnih delcev; (- - -) teoretične vrednosti dobljene z upoštevanjem dielektrične polarizacije; (x) Scofield [3, 46]. Vrednosti v tabeli so deljene s potenčno funkcijo, ki se najbolje prilagaja meritvam.
) eksperimentalne vrednosti; (---) model neodvisnih delcev; (- - -) teoretične vrednosti dobljene z upoštevanjem dielektrične polarizacije; (x) Scofield [3, 46]. Vrednosti v tabeli so deljene s potenčno funkcijo, ki se najbolje prilagaja meritvam.
Drobne strukture
Večelektronske drobne strukture nad robovi L postanejo dobro vidne šele pri nadaljnji povečavi. Na slikah 15, 16 in 17 sta za vsak rob označena izseka A in B iz spektra, ki sta v nadaljevanju predstavljena pobliže. Vse večelektronske drobne strukture, ki jih je pri doseženi občutljivosti meritev še moč opaziti, so zajete v energijskem intervalu, ki ga nad vsakim robom pokrivata označena izseka. Potek preseka izven teh intervalov je gladek v okviru statističnega šuma meritve.
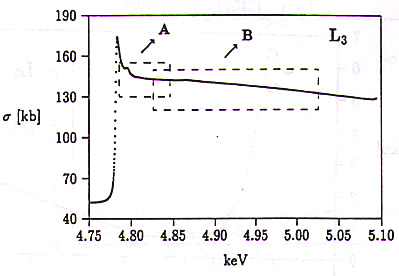
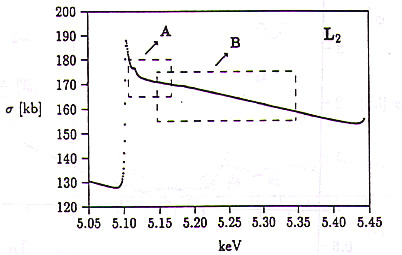
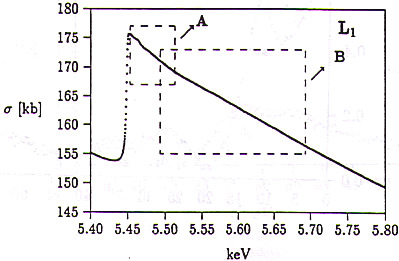
Slike 15, 16, 17: Potek preseka za fotoabsorpcijo nad robovi L. Nad vsakim robom sta označena izseka A in B, ki sta v nadaljevanju predstavljena podrobneje.
Na sliki 18 je za vsak rob povečano predstavljen izsek A. Od izmerjenega spektra je v vseh treh primerih odštet asimptotski naklon spektra na energijskem intervalu izseka. Energijska skala je relativna glede na energijo posameznega roba. Energijski interval izseka je v vseh treh primerih enak, razlikuje pa se povečava, saj so absolutne spremembe v preseku nad robom L![]() skoraj za red velikosti večje kot nad L
skoraj za red velikosti večje kot nad L![]() . Drobne strukture so označene s črkami od a do e.
. Drobne strukture so označene s črkami od a do e.
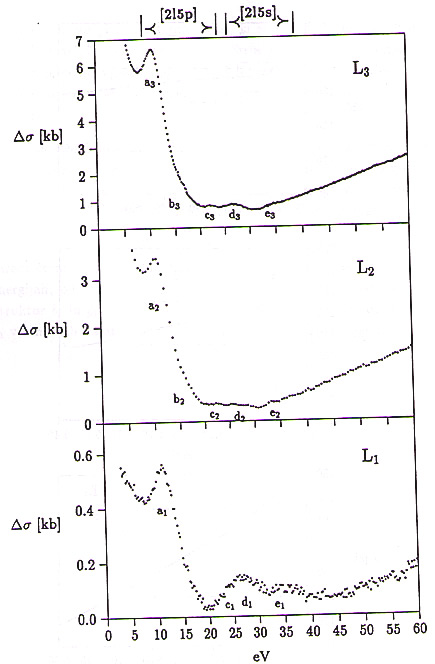
Slika 18: (Izsek A) Povečan prikaz energijskega poteka preseka v izseku {\bf A} nad robovi L. Od izmerjenega spektra je v vseh treh primerih odštet asimptotski naklon. Drobne strukture so označene s črkami od a do e. Označena sta tudi energijska intervala s pragovi ekscitacij [2l5p] in [2l5s].
Z odštevanjem asimptotskega naklona na lokalnem odseku spektra dosežemo minimalno popačenje drobnih struktur, vendar ta postopek ne daje potrebne povečave. Na slikah od 17 do 19 je predstavljen isti energijski izsek A, pri čemer je namesto premice od originalnega spektra odšteta gladka krivulja oblike
(22)) |
kjer je E energija, a![]() pa so konstantni koeficienti. Z eksponentno funkcijo v izrazu (22) opišemo približevanje izmerjenega energijskega poteka neposredno nad robom k povprečnemu naklonu pri višjih energijah. Vrednost koeficientov je za vsak rob posebej določena numerično, z nelinearno metodo najmanjših kvadratov (metoda Levenberg-Marquardt [48] ), tako da se krivulja najbolje prilagaja izmerjenemu spektru na celotnem intervalu izseka. Analitična oblika uporabljene funkcije zagotavlja, da pri prilagajanju izmerjenim spektrom funkcija ne more slediti posameznim drobnim strukturam, ampak reproducira le globalni potek. Ko tako dobljen globalni potek odštejemo, ostanejo v spekru le drobne strukture in s tem postane njihova oblika bistveno bolj pregledna. Namesto absolutnih sprememb preseka
pa so konstantni koeficienti. Z eksponentno funkcijo v izrazu (22) opišemo približevanje izmerjenega energijskega poteka neposredno nad robom k povprečnemu naklonu pri višjih energijah. Vrednost koeficientov je za vsak rob posebej določena numerično, z nelinearno metodo najmanjših kvadratov (metoda Levenberg-Marquardt [48] ), tako da se krivulja najbolje prilagaja izmerjenemu spektru na celotnem intervalu izseka. Analitična oblika uporabljene funkcije zagotavlja, da pri prilagajanju izmerjenim spektrom funkcija ne more slediti posameznim drobnim strukturam, ampak reproducira le globalni potek. Ko tako dobljen globalni potek odštejemo, ostanejo v spekru le drobne strukture in s tem postane njihova oblika bistveno bolj pregledna. Namesto absolutnih sprememb preseka ![]() so podane relativne spremembe preseka glede na presek za ionizacijo ustrezne podlupine L na robu
so podane relativne spremembe preseka glede na presek za ionizacijo ustrezne podlupine L na robu ![]() .
.
Izseki B iz vsakega od spektrov so prikazani na sliki 19. Tudi v tem primeru je energijski interval za vse tri robove enak, energijska skala je relativna glede na energijo posameznega roba, povečava je prilagojena velikosti drobnih struktur. Zaradi preglednosti je v primeru robov L![]() in L
in L![]() od originalnega spektra odštet srednji parabolični globalni potek. Nad robom L
od originalnega spektra odštet srednji parabolični globalni potek. Nad robom L![]() , pa je odštet le asimptotski naklon spektra na izseku. Drobne strukture so označene s črkami od f do h.
, pa je odštet le asimptotski naklon spektra na izseku. Drobne strukture so označene s črkami od f do h.
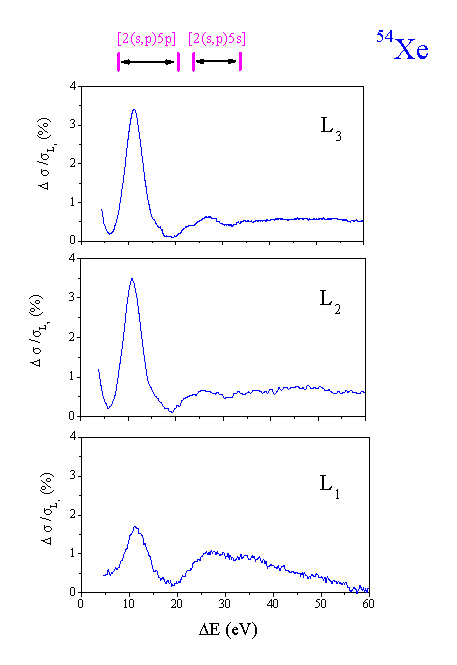
Slika 19: (Izsek A)Od originalnega spektra so odštete vrednosti funkcije (22), ki se najbolje prilagaja meritvam na izseku A. Vrednosti preseka ![]() so podane relativno glede na velikost preseka za ionizacijo ustrezne podlupine L na robu
so podane relativno glede na velikost preseka za ionizacijo ustrezne podlupine L na robu ![]() . Oznake v sliki imajo isti pomen kot na sliki 18.
. Oznake v sliki imajo isti pomen kot na sliki 18.
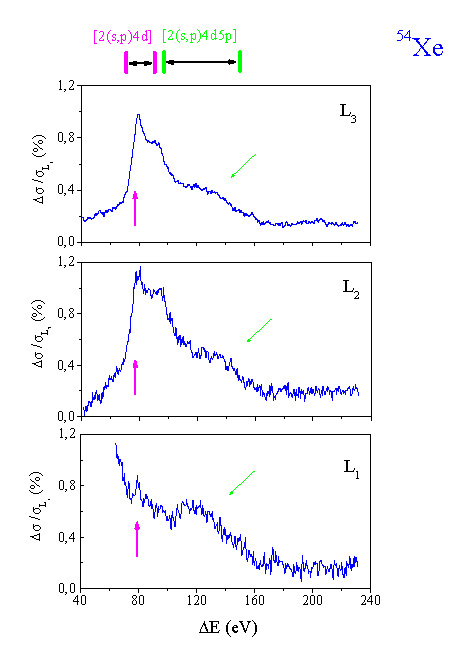
Slika 20: (Izsek B) Povečan prikaz energijskega poteka preseka v izseku B nad robovi L. V primeru robov L![]() in L
in L![]() je od izmerjenega spektra odštet povprečni parabolični potek, na robom L
je od izmerjenega spektra odštet povprečni parabolični potek, na robom L![]() pa asimptotski naklon na izseku. Drobne strukture so označene z f,g in h. Označeni so tudi energijski intervali, na katerih postanejo energijsko dovoljene dvojne ekscitacije [2l4d] in [2l4p] ter trojne ekscitacije [2l4d5p].
pa asimptotski naklon na izseku. Drobne strukture so označene z f,g in h. Označeni so tudi energijski intervali, na katerih postanejo energijsko dovoljene dvojne ekscitacije [2l4d] in [2l4p] ter trojne ekscitacije [2l4d5p].
Relativne energije ![]() označenih drobnih struktur, glede na izmerjeno ionizacijsko energijo ustrezne podlupine L, so zbrane v tabelah 2, 3 in 4 za vsak rob L posebej. Strukture a, d, in f, imajo značilno obliko resonančne črte, ki jo opišemo z Lorentzovo krivuljo. Njihove relativne energije so določene s prilagajanjem Lorentzove krivulje vsaki od struktur, po nelinearni metodi najmanjših kvadratov. Iz parametrov Lorentzove krivulje je poleg lege črte določena tudi njena širina na polovični višini
označenih drobnih struktur, glede na izmerjeno ionizacijsko energijo ustrezne podlupine L, so zbrane v tabelah 2, 3 in 4 za vsak rob L posebej. Strukture a, d, in f, imajo značilno obliko resonančne črte, ki jo opišemo z Lorentzovo krivuljo. Njihove relativne energije so določene s prilagajanjem Lorentzove krivulje vsaki od struktur, po nelinearni metodi najmanjših kvadratov. Iz parametrov Lorentzove krivulje je poleg lege črte določena tudi njena širina na polovični višini ![]() ter njena višina
ter njena višina ![]() . V tabelah so višine struktur podane relativno, glede na velikost polnega preseka za fotoabsorpcijo
. V tabelah so višine struktur podane relativno, glede na velikost polnega preseka za fotoabsorpcijo ![]() na ustrezni podlupini
na ustrezni podlupini ![]() pri energiji strukture. Strukture c in e lahko okarakteriziramo kot skoke v preseku, ki jih opišemo z integralom Lorentzove krivulje. Strukture g in h se raztezajo čez bistveno širši energijski interval. Zanje nimamo fizikalnega modela. Vrednosti za njihovo lego, širino na polovični višini in relativno višino, ki so podane v tabelah 2 do 4, so dobljene z aproksimacijo z Gaussovo krivuljo. Struktura {\em b} se nad roboma L
pri energiji strukture. Strukture c in e lahko okarakteriziramo kot skoke v preseku, ki jih opišemo z integralom Lorentzove krivulje. Strukture g in h se raztezajo čez bistveno širši energijski interval. Zanje nimamo fizikalnega modela. Vrednosti za njihovo lego, širino na polovični višini in relativno višino, ki so podane v tabelah 2 do 4, so dobljene z aproksimacijo z Gaussovo krivuljo. Struktura {\em b} se nad roboma L![]() in L
in L![]() kaže kot šibek greben na višjeenergijski strani resonančne črte a. Njena relativna energija je določena pri podmeni, da gre za šibko resonančno črto, ki je zlita z dominantno resonanco a.
kaže kot šibek greben na višjeenergijski strani resonančne črte a. Njena relativna energija je določena pri podmeni, da gre za šibko resonančno črto, ki je zlita z dominantno resonanco a.
Pri doseženi povečavi vidimo, da sta energijska poteka preseka nad roboma L![]() in L
in L![]() popolnoma skladna. Vse drobne strukture se ujemajo tako po relativni energiji, kot po obliki in relativni velikosti. Do nivoja šuma meritev ni opaziti nobenih ključnih razlik. Zato bomo v nadaljevanju oba roba obravnavali skupaj in ju označevali z L
popolnoma skladna. Vse drobne strukture se ujemajo tako po relativni energiji, kot po obliki in relativni velikosti. Do nivoja šuma meritev ni opaziti nobenih ključnih razlik. Zato bomo v nadaljevanju oba roba obravnavali skupaj in ju označevali z L![]() .
.
Nad robom L![]() je slika drugačna. Prepoznamo sicer lahko sovpadne strukture zaradi česar smo uporabili enake črkovne oznake. Nastopajo pri enakih relativnih energijah, od struktur L
je slika drugačna. Prepoznamo sicer lahko sovpadne strukture zaradi česar smo uporabili enake črkovne oznake. Nastopajo pri enakih relativnih energijah, od struktur L![]() pa se lahko razlikujejo po relativni velikosti in širini. Struktur b
pa se lahko razlikujejo po relativni velikosti in širini. Struktur b![]() in g
in g![]() znotraj meje občutljivosti ni opaziti. Pač pa so strukture d
znotraj meje občutljivosti ni opaziti. Pač pa so strukture d![]() ,e
,e![]() in h
in h![]() v osnovnih parametrih podobne analognim strukturam nad L
v osnovnih parametrih podobne analognim strukturam nad L![]() .
.
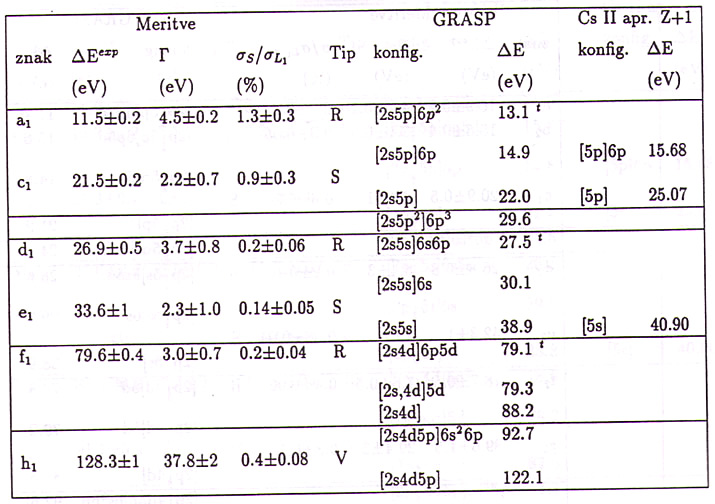
Tabela 2: Identifikacija drobnih struktur nad absorpcijskim robom L![]() . Za vsako od struktur od a do h je podana relativna energija
. Za vsako od struktur od a do h je podana relativna energija ![]() glede na ionizacijsko energijo podlupine L
glede na ionizacijsko energijo podlupine L![]() (5452.9 eV), širina
(5452.9 eV), širina ![]() ter relativna višina
ter relativna višina ![]() . Označen je tip posamezne drobne strukture: R -- Resonanca; S -- Skok; V -- Veleresonanca. Podane so izračunane energije tistih dvoelektronskih in trielektronskih prehodov, ki so potrebni za identifikacijo drobnih struktur, relativno glede na izračunano ionizacijsko energijo podlupine L
. Označen je tip posamezne drobne strukture: R -- Resonanca; S -- Skok; V -- Veleresonanca. Podane so izračunane energije tistih dvoelektronskih in trielektronskih prehodov, ki so potrebni za identifikacijo drobnih struktur, relativno glede na izračunano ionizacijsko energijo podlupine L![]() . Indeks
. Indeks ![]() pri resonančnih prehodih označuje, da se vrednost nanaša na težišče multipleta, ki pripada izbrani konfiguraciji, v ostalih primerih je podana energija najnižjega stanja v multipletu. Za primerjavo so dodane energije, dobljene z aproksimacijo Z+1 [49].
pri resonančnih prehodih označuje, da se vrednost nanaša na težišče multipleta, ki pripada izbrani konfiguraciji, v ostalih primerih je podana energija najnižjega stanja v multipletu. Za primerjavo so dodane energije, dobljene z aproksimacijo Z+1 [49].
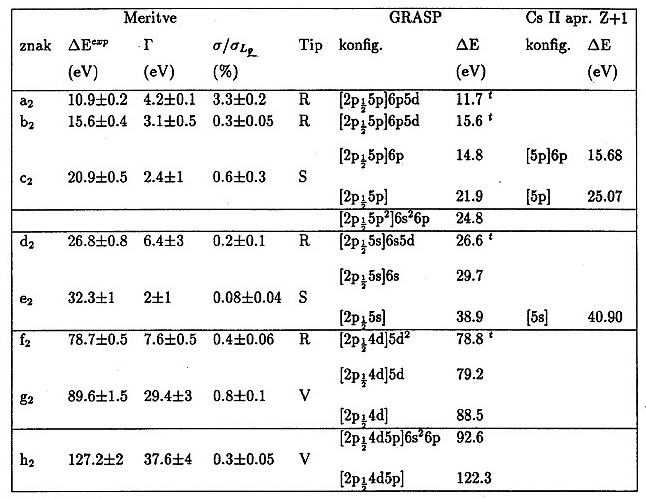
Tabela 3: Identifikacija drobnih struktur nad absorpcijskim robom L![]() . Pomen oznak je isti kot v tabeli 2. Energije drobnih struktur so podane relativno na ionizacijsko energijo podlupine L
. Pomen oznak je isti kot v tabeli 2. Energije drobnih struktur so podane relativno na ionizacijsko energijo podlupine L![]() (5107.0 eV).
(5107.0 eV).
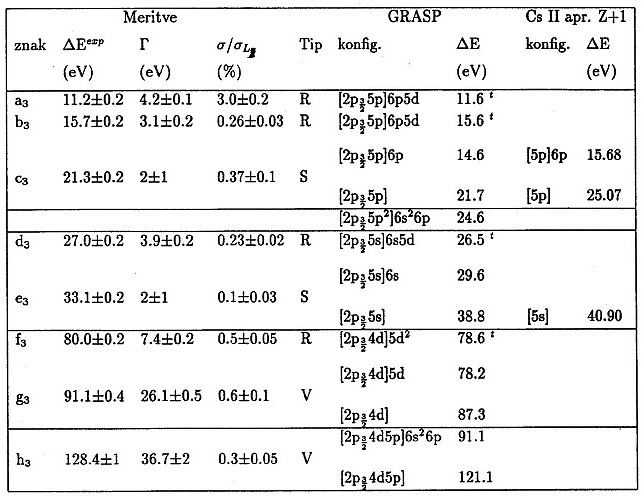
Tabela 4: Identifikacija drobnih struktur nad absorpcijskim robom L![]() . Pomen oznak je isti kot v tabeli 2. Energije drobnih struktur so podane relativno na ionizacijsko energijo podlupine L
. Pomen oznak je isti kot v tabeli 2. Energije drobnih struktur so podane relativno na ionizacijsko energijo podlupine L![]() (4786.3 eV).
(4786.3 eV).
Energijska indentifikacija drobnih struktur
Popolna analiza drobnih struktur v absorpcijskih spektrih je opravljena šele s teoretično rekonstrukcijo preseka. V prvem koraku take analize identificiramo večelektronske drobne strukture po energiji, pri kateri se v spektru pojavijo. Primerjava z izračunanimi energijami večelektronskih prehodov pokaže, katere ekscitacije so pri energiji dane drobne strukture možne in bi lahko prispevale k njenemu nastanku. Po zgledu dosedanjih analiz bomo sistematično pregledali nabor vseh razpoložljivih dvoelektronskih ekscitacij, ki ustrezajo izbirnim pravilom. V nekaterih primerih pa zajema izbor tudi trielektronske ekscitacije.
Na slikah 18, 19 in 20 so označeni energijski intervali, na katerih lahko pričakujemo hkratne ekscitacije zunanjih elektronov 5p, 5s, 4d in 4p ob tvorbi vrzeli v podlupini L. Strukture, ki jih tolmačimo z udeležbo dane zunanje lupine, so omejene na interval, ki se začne z najnižjo možno resonančno ekscitacijo in se konča s pragom za ionizacijo udeleženih elektronov. Seveda prispevajo večelektronski prehodi v ionizirana stanja (''shake-up'' in ''shake-off'') k preseku pri vseh energijah nad pragom, vendar se ostre strukture, merljive v absorpcijskih spektrometriji, lahko pojavijo le v tem intervalu. Izračunane energije prehodov, ki definirajo meje intervalov za posamezne zunanje podlupine, se v relativni skali, glede na ionizacijsko energijo ustrezne podlupine L, ujemajo za vse tri robove L v okviru 1 eV.
Primerjava z izračunanimi energijami dvojnih prehodov kaže, da so za nastanek struktur a,b in c možni kandidati le hkratne ekscitacije elektrona 5p ob tvorbi vrzeli v podlupini L. Strukturi d in e sovpadata z intervalom, kjer postanejo energijsko dovoljene dvojne ekscitacije [2l5s] ter trojne ekscitacije [2l5p![]() ]. Prispevki trojnih ekscitacij so zaradi multipletnosti končnih stanj znatno bolj razmazani kot prispevki dvojnih ekscitacij. To pomeni, da se pri postopku analize dodatno razmažejo, zato jih pri interpretaciji ne bomo uporabili. Strukturi f in g se pojavita na energijskem intervalu, kjer po izračunanih energijah pričakujemo dvojne ekscitacije elektronov L in 4d. široke strukture h z dvoelektronskimi ekscitacijami ne moremo pojasniti. Po energiji jo lahko pripišemo trielektronskim ekscitacijam, pri katerih sodelujeta poleg elektrona iz ustrezne podlupine L še po en elektron iz podlupine 4d in podlupine 5p.
]. Prispevki trojnih ekscitacij so zaradi multipletnosti končnih stanj znatno bolj razmazani kot prispevki dvojnih ekscitacij. To pomeni, da se pri postopku analize dodatno razmažejo, zato jih pri interpretaciji ne bomo uporabili. Strukturi f in g se pojavita na energijskem intervalu, kjer po izračunanih energijah pričakujemo dvojne ekscitacije elektronov L in 4d. široke strukture h z dvoelektronskimi ekscitacijami ne moremo pojasniti. Po energiji jo lahko pripišemo trielektronskim ekscitacijam, pri katerih sodelujeta poleg elektrona iz ustrezne podlupine L še po en elektron iz podlupine 4d in podlupine 5p.
Naravna širina in multipletnost končnih stanj omejujeta podrobnejšo identifikacijo drobnih struktur. Naravno širino končnih stanj pri dvoelektronskih prehodih lahko ocenimo z naravno širino končnih stanj pri enojnih prehodih elektrona L v vezana stanja:
![]()
![]()
![]()
![]() 3eV. V izmerjenih spektrih torej ne moremo ločiti dvoelektronskih prehodov, ki se po energiji razlikujejo za manj kot 3 eV.
3eV. V izmerjenih spektrih torej ne moremo ločiti dvoelektronskih prehodov, ki se po energiji razlikujejo za manj kot 3 eV.
Razlike med izračunanimi energijami prehodov v bližnja višja vzbujena stanja so tipično manjše od naravne širine. Poleg tega pride tudi do prekrivanja med multipleti, ki pripadajo konfiguracijam teh končnih stanj. Navajanje energij prehodov v vsa mogoča končna stanja, ki se razlikujejo za manj kot je naravna širina, ni smiselno, ker vseh teh prehodov v absorpcijskih spektrih niti v načelu ni mogoče ločiti.
Z večjo zanesljivostjo lahko podrobneje identificiramo le resonančne črte. Njihova energijska širina je primerljiva z naravno širino. V spektru jih je mogoče dobro ločiti od ostalih drobnih struktur. Pojasnimo jih lahko z diskretnimi ekscitacijami obeh elektronov v nezasedena vezana stanja. Po prejšnjem zadošča, da se pri izbiri možnih diskretnih dvoelektronskih prehodov, ki bi lahko prispevali k nastanku posamezne resonance, omejimo na najverjetnejše, to je tiste, pri katerih preide en elektron v najnižje nezasedeno stanje dipolno, drugi pa monopolno.
Dvoelektronske ekscitacije [2l5p] in [2l5s]
Od drobnih struktur, ki ustrezajo dvojnim ekscitacijam elektronov 2l in 5p, je nad vsakim robom L dobro prepoznavna resonančna črta a. Nad roboma L![]() jo pripišemo dvoelektronskim prehodom v stanja [2p5p]6p5d, nad robom L
jo pripišemo dvoelektronskim prehodom v stanja [2p5p]6p5d, nad robom L![]() pa v [2s5p]6p
pa v [2s5p]6p![]() . Na sliki 21 je za vsako od konfiguracij prikazan razpored nivojev v pripadajočem multipletu. Narisani so samo tisti nivoji, ki zadoščajo izbirnim pra\-vilom pri prehodu, torej tisti, pri katerih je celotna vrtilna količina J=1 ter parnost pozitivna. Pri podlupinah L
. Na sliki 21 je za vsako od konfiguracij prikazan razpored nivojev v pripadajočem multipletu. Narisani so samo tisti nivoji, ki zadoščajo izbirnim pra\-vilom pri prehodu, torej tisti, pri katerih je celotna vrtilna količina J=1 ter parnost pozitivna. Pri podlupinah L![]() je multiplet razcepljen na dva asimetrična dela z razmikom težišč 3.5 eV in s približno 2 eV široko energijsko vrzeljo. Težišče prvega dela multipleta, v katerem je večina nivojev, se v okviru 1 eV ujema z energijo resonance a
je multiplet razcepljen na dva asimetrična dela z razmikom težišč 3.5 eV in s približno 2 eV široko energijsko vrzeljo. Težišče prvega dela multipleta, v katerem je večina nivojev, se v okviru 1 eV ujema z energijo resonance a![]() , medtem ko se težišče drugega dela multipleta s štirimi nivoji ujema z energijo šibke resonance b
, medtem ko se težišče drugega dela multipleta s štirimi nivoji ujema z energijo šibke resonance b![]() (tabeli 2 in 3). Pri podlupini L
(tabeli 2 in 3). Pri podlupini L![]() takega razcepa ni in tudi šibke resonance b
takega razcepa ni in tudi šibke resonance b![]() ni opaziti na višjeenergijski strani resonance a
ni opaziti na višjeenergijski strani resonance a![]() . Težišče multipleta se razlikuje od energije resonance a
. Težišče multipleta se razlikuje od energije resonance a![]() za približno 1.5 eV (Tabela 4). Tolikšno razhajanje je še mogoče pripisati nenatančnosti pri računanju energij dvoelektronskih prehodov. Energijska širina posameznih multipletov je, pri naravni širini posameznih stanj
za približno 1.5 eV (Tabela 4). Tolikšno razhajanje je še mogoče pripisati nenatančnosti pri računanju energij dvoelektronskih prehodov. Energijska širina posameznih multipletov je, pri naravni širini posameznih stanj ![]() = 3eV, primerljiva z izmerjeno energijsko širino pripadajočih resonanc.
= 3eV, primerljiva z izmerjeno energijsko širino pripadajočih resonanc.
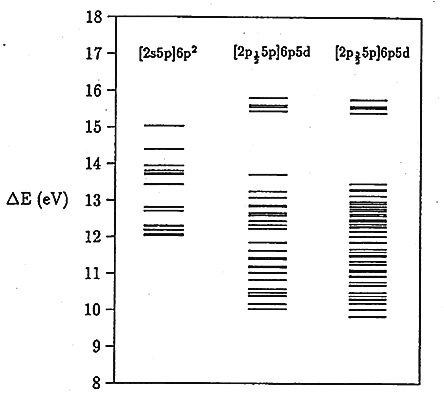
Slika 21: Razpored atomskih nivojev J![]() = 1
= 1![]() v multipletih, ki pripadajo konfiguracijam [2s5p]6p
v multipletih, ki pripadajo konfiguracijam [2s5p]6p![]() , [2p
, [2p![]() 5p]6p5d in [2p
5p]6p5d in [2p![]() 5p]6p5d.
5p]6p5d.
Prispevkov dvojnih resonančnih prehodov v višja Rydbergova stanja k resonancam a ne moremo ločiti, ker se po energiji premalo razlikujejo od prehodov v najnižja prosta stanja. Rydbergova serija [2s5p]6pnp oziroma [2p5p]6pnd, ki se začne s konfiguracijo [2s5p]6p![]() oziroma [2p5p]6p5d, se izteče znotraj intervala 3 eV (tabele 2, 3 oziroma 4).
oziroma [2p5p]6p5d, se izteče znotraj intervala 3 eV (tabele 2, 3 oziroma 4).
Podobno kot pri dvoelektronskih prehodih [2l5p] se tudi območje ekscitacij [2l5s] začne z diskretnimi prehodi, ki se kažejo v obliki resonančne črte d. Resonanca d je približno za red velikosti šibkejša od resonance a. Dobro je prepoznavna nad robom L![]() , medtem ko jo je nad roboma L
, medtem ko jo je nad roboma L![]() in L
in L![]() zaradi relativne šibkosti težko ločiti od sosednje strukture c. Nad roboma L
zaradi relativne šibkosti težko ločiti od sosednje strukture c. Nad roboma L![]() pripišemo resonanco d dvoelektronskim prehodom v stanja [2p5s]6s5d, nad robom L
pripišemo resonanco d dvoelektronskim prehodom v stanja [2p5s]6s5d, nad robom L![]() pa [2s5s]6s6p. Težišče multipleta, ki pripada tem konfiguracijam, se v vseh treh primerih po energiji dobro ujema z njenim težiščem (tabele 2, 3, 4). Dvoelektronski resonančni prehodi v višja Rydbergova stanja se, tako kot pri resonanci a, zvrstijo znotraj naravne širine in so zato v meritvah nerazločljivi.
pa [2s5s]6s6p. Težišče multipleta, ki pripada tem konfiguracijam, se v vseh treh primerih po energiji dobro ujema z njenim težiščem (tabele 2, 3, 4). Dvoelektronski resonančni prehodi v višja Rydbergova stanja se, tako kot pri resonanci a, zvrstijo znotraj naravne širine in so zato v meritvah nerazločljivi.
Struktura c sovpada z izračunano energijo praga za dvojno ionizacijo podlupin L in 5p. Vendar skokovitega porasta preseka c ne moremo pripisati dvojni ionizaciji [2l5p], ker doseže presek zanjo polno vrednost šele na intervalu ~ 20 eV nad pragom, ne pa skokovito. Tudi skokovite spremembe preseka e z energijsko analizo ne moremo podrobneje identificirati, ker po energiji ne ustreza nobenemu končnemu stanju s preprosto konfiguracijo.
Ekscitacije [2l4d] in [2l4d5p]
Na intervalu, kjer postanejo energijsko dovoljene hkratne ekscitacije podlupine 4d ob tvorbi vrzeli v podlupini L, je nad vsemi robvi L prisotna resonančna črta f, ki je posledica diskretnih prehodov elektrona L in 4d v vezana stanja. Nad resonancama f![]() opazimo široko strukturo g.
opazimo široko strukturo g.
Podatki iz tabel 2 do 4 kažejo, da se lega resonančne črte f dobro ujema z energijo dvoelektronskih prehodov v stanja [2p4d]5d![]() oziroma [2s4d]6p5d. V absorpcijski spektrometriji žlahtnih plinov je to prvi primer resonance z udeležbo nivojev d. Relativno velika širina resonance f
oziroma [2s4d]6p5d. V absorpcijski spektrometriji žlahtnih plinov je to prvi primer resonance z udeležbo nivojev d. Relativno velika širina resonance f![]() ~ 7 eV je razumljiva, ker sta v končnem stanju odprti dve podlupini d, ki se sestavljata v multiplet s širino ~ 5.0 eV. šibka resonanca f
~ 7 eV je razumljiva, ker sta v končnem stanju odprti dve podlupini d, ki se sestavljata v multiplet s širino ~ 5.0 eV. šibka resonanca f![]() predstavlja izjemo s širino, ki je enaka naravni.
predstavlja izjemo s širino, ki je enaka naravni.
Struktura g![]() sovpada z območjem prehodov v ionizirana stanja [2p4d], ne kaže pa značilne oblike skoka. Nasploh kažejo absorpcijski skoki z udeležbo lupine d nad robom K kriptona in ksenona izrazito razmazanost, tako da je netipična oblika strukture g
sovpada z območjem prehodov v ionizirana stanja [2p4d], ne kaže pa značilne oblike skoka. Nasploh kažejo absorpcijski skoki z udeležbo lupine d nad robom K kriptona in ksenona izrazito razmazanost, tako da je netipična oblika strukture g![]() artefakt analize. Analogne strukture g
artefakt analize. Analogne strukture g![]() ni mogoče zanesljivo izluščiti, čeprav jo oblika spektra dopušča v velikosti, ki bi ustrezala razmerju f
ni mogoče zanesljivo izluščiti, čeprav jo oblika spektra dopušča v velikosti, ki bi ustrezala razmerju f![]() /f
/f![]() .
.
Širok greben h po energiji ustreza trielektronskim ekscitacijam [2l4d5p]. Dokaz o obstoju analognih trielektronskih ekscitacijah so nedavno odkrili tudi v spektru totalnega preseka za fotoabsorpcijo na lupini K kriptona [50]. Opazili so šibek absorpcijski rob, ki se pojavi pri energiji praga za trojno ionizacijo [1s3d4p]. V obeh primerih gre torej za hkratno ionizacijo elektronov iz zunanjih podlupin d in p ob fotoabsorpciji na notranji lupini.
Energijski potek preseka pri strukturi h je zelo podoben tistemu pri pragu za direktno fotoionizacijo podlupine 4d v ultravijoličnem področju (slika 22). nad pragom 4d se presek dvigne v širok vrh, ki se po širini (~40 eV) ujema s širino strukture h (37 eV). V teorijski analizi so nenavadni energijski potek preseka za fotoionizacijo podlupine 4d pojasnili z relaksacijo atomskih orbital ob nastanku vrzeli v podlupini 4d ter z neelastičnim sipanjem fotoelektrona na zunanjih elektronih 5p [51, 52]. Ko preseže kinetična energija fotoelektrona 4d ionizacijsko energijo podlupine 5p, prispevajo dvojne ekscitacije [4d5p] znaten delež polnega preseka.
Podobnost obeh energijskih potekov v okolici praga za direktno oziroma posredno vzbujanje podlupin 4d in 5p kaže, da so korelacije med elektroni 4d in 5p tako močne, da določajo energijski potek ekscitacij neodvisno od način vzbuditve.
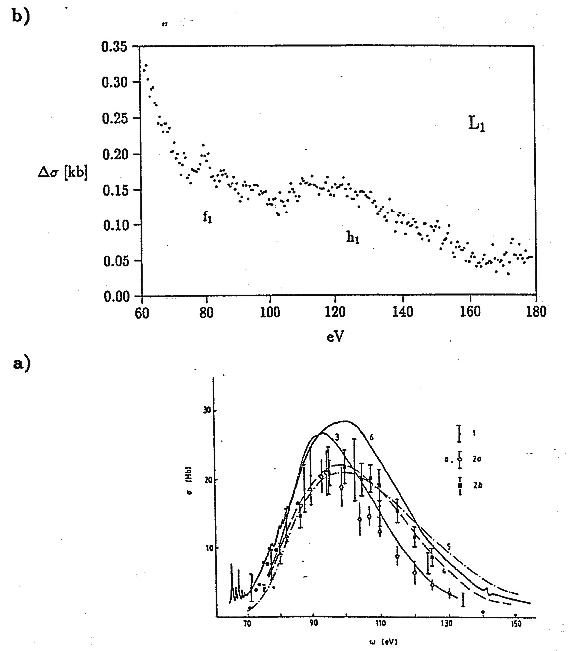
Slika 22: a) Presek za fotoabsorpcijo v ksenonu v okolici praga za fotoionizacijo podlupine 4d v ultravijoličnem področju. S polno črto (6) je označen izmerjeni polni presek. Eksperimentalne vrednosti za presek za fotoionizacijo podlupine 4d so podane z znaki (1, 2a, 2b), različne teoretične vrednosti zanj pa s krivuljami (3, 4 in 5) [51, 52]. Pod pragom za ionizacijo podlupine 4d pri 68.3 eV so v polnem preseku prisotne resonančne črte, ki so posledica diskretnih prehodov elektrona 4d v vezana stanja. Nad pragom za dvojno ionizacijo [4d5p] se polni presek poveča v primerjavi s presekom za enojno fotoionizacijo podlupine 4d. Razliko prispevajo dvojne ekscitacije [4d5p]. b) Presek za fotoabsorpcijo nad absorpcijskim robom L![]() pri energiji praga za trojno ionizacijo [2s4d5p]. Energijski skali obeh spektrov ({\bf a)} in {\bf b)}) sta premaknjeni tako, da sovpadata praga za nastanek obojih struktur.
pri energiji praga za trojno ionizacijo [2s4d5p]. Energijski skali obeh spektrov ({\bf a)} in {\bf b)}) sta premaknjeni tako, da sovpadata praga za nastanek obojih struktur.
Zgornja meja presekov za dvoelektronske prehode [2l4p], [2l4s] in [2l3d]
V tabeli 5 je za vsako od podlupin L podan energijski interval, na katerem se odpro reakcijski kanali dvoelektronskih prehodov, ki vključujejo podlupine 4p, 4s oziroma 3d. V izmerjenih spektrih na omenjenih energijskih intervalih ne moremo zanesljivo razbrati nobenih drobnih struktur nad gladkim potekom preseka. Po izkušnjah iz meritev absorpcijskih spektrov K in po teorijskih argumentih lahko to pripišemo dvema vzrokoma. Dodatne ekscitacije elektronov iz globljih podlupin so bistveno manj verjetne kot ekscitacije zunanjih šibko vezanih podlupin, poleg tega v njih prevladujejo prehodi ''shake-off'' \cite{carlson}, ki jih postopek analize zabriše.
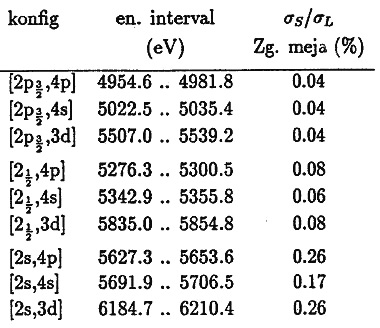
Tabela 5: Energijski intervali, na katerih postanejo energijsko dovoljene hkratne ekscitacije podlupin 4p, 4s oziroma 3d ob fotoabsorpciji v podlupinah L. Za vsak interval je označena zgornja meja za relativno velikost preseka za dvoelektronske ekscitacije, ki je ocenjena iz statističnega šuma meritve na intervalu.
Rezultati iz robov K argona in kriptona kažejo, da je relativne velikosti presekov za dvojne ionizacije na notranjih lupinah mogoče oceniti v približku nenadnega prehoda. Teoretične napovedi v okviru modela ''otresanja'' za verjetnosti za ionizacijo v podlupinah L ksenona z dodatno vzbuditvijo ali ionizacijo so zbrane v tabeli 6. Podane so v deležu polnega preseka za fotoabsorpcijo v izbrani podlupini. Tabelirane vrednosti kažejo, da so hkratne ekscitacije v notranjih podlupinah 3d, 4s in tudi 4p skoraj za red velikosti manj verjetne od tistih v zunanjih podlupinah 5p, 5s in 4d. Z oceno, da je pri dvojnih ekscitacijah [2l4p], [2l4s] ter [2l3d] v ksenonu razmerje med verjetnostjo za prehode ''shake-up'' proti verjetnosti za prehode ''shake-off'' približno 1 : 8, kot v primeru dvojnih ekscitacij [1s3p] v kriptonu [53] ter [1s2p] v argonu [54], lahko iz tabeliranih vrednosti za te dvoelektronske ekscitacije ocenimo velikosti absorpcijskih skokov. Vrednosti, ki jih s tako oceno dobimo so reda velikosti 10![]() %.
%.

Tabela 6: Verjetnosti za hkratno ekscitacijo elektrona iz podlupine nl (%), kot posledica nenadnega nastanka vrzeli v eni od podlupin L [31]
Iz velikosti statističnega šuma v spektru na omenjenih intervalih lahko podamo zgornjo mejo za velikost neopaženih drobnih struktur. V absolutni skali je velikost statističnega šuma na vseh intervalih približno enaka in znaša ![]() 15 barn. Pri ocenjevanju zgornje meje za drobne strukture predpostavimo, da bi jih v izmerjenih spektrih zanesljivo opazili, če bi po velikosti presegale polno amplitudo šuma, to je približno 30 barn. Od tod izpeljemo zgornje meje za relativne velikosti preseka za dvoelektronske ekscitacije v tabeli 5. Ocenjene eksperimentalne zgornje meje niso manjše od teoretičnih ocen velikosti, kar dopusti možnost, da so drobne strukture zaradi dvoelektronskih prehodov [2l4p], [2l4s] ter [2l3d] skrite v statističnem šumu meritve.
15 barn. Pri ocenjevanju zgornje meje za drobne strukture predpostavimo, da bi jih v izmerjenih spektrih zanesljivo opazili, če bi po velikosti presegale polno amplitudo šuma, to je približno 30 barn. Od tod izpeljemo zgornje meje za relativne velikosti preseka za dvoelektronske ekscitacije v tabeli 5. Ocenjene eksperimentalne zgornje meje niso manjše od teoretičnih ocen velikosti, kar dopusti možnost, da so drobne strukture zaradi dvoelektronskih prehodov [2l4p], [2l4s] ter [2l3d] skrite v statističnem šumu meritve.
| |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||