EXAFS

NANO SKUPKI

 

 

ANALIZA SIGNALA EXAFS

Oglejmo si postopek luščenja strukturnega signala EXAFS na primeru kobaltovega absorpcijskega spektra μ(E), izmerjenega s sinhrotronsko svetlobo (slika 10). Kot smo pojasnili že v uvodnem poglavju, je signal EXAFS nad robom K posledica modulacije preseka za fotoefekt v lupini K. Iz celotne absorpcije moramo torej v prvem koraku izločiti prispevek lupine K:

(1.20)

Prispevke preostalih elektronskih lupin in morebitne prispevke drugih elementov v vzorcu lahko določimo v energijskem področju pred absorpcijskim robom. Njihov energijski potek dobro opišemo s potenčno funkcijo , kjer je α tipično med 3 in 4. Parametre poskusne funkcije določimo s prilagajanjem izmerjenim vrednostim pred robom in dobljeno funkcijo ekstrapoliramo na energijsko področje nad robom. Ker je ekstrapolacija potenčne funkcije, ki jo določimo s prilagajanjem na relativno ozkem intervalu točk pred robom, lahko nestabilna, pogosto za oceno raje uporabimo kar linearno funkcijo.

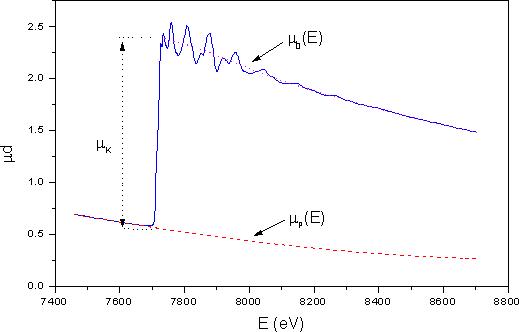
Slika 10. Postopek luščenja signala EXAFS iz absorpcijskega spektra, prikazan na primeru absorpcijskega spektra kovinskega kobalta, ki je bil izmerjen s sinhrotronsko svetlobo v laboratoriju HASYLAB, DESY v Hamburgu. V spektru je označena velikost skoka absorpcijskega roba K kobalta. Črtkana črta prikazuje prispevke preostalih elektronskih lupin k celotni absorpciji. Gladek potek absorpcijskega koeficienta brez strukturnega signala nad robom je označen s pikčasto čtrto.

Signal EXAFS izračunamo po definiciji:

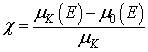(1.21)

.kjer je velikost skoka na robu K, pa energijski potek absorpcijskega koeficienta brez strukturnega signala, ki ga opišemo z neko gladko funkcijo (na primer s polinomom tretje ali četrte stopnje ali pa z zlepkom polinomskih funkcij), ki se najbolje prilega izmerjenemu spekru v celotnem energijskem področju nad robom.

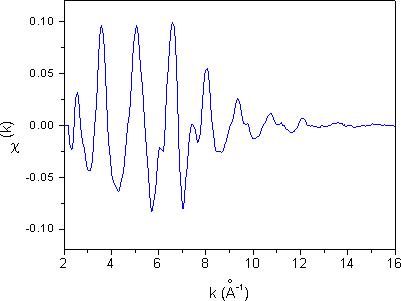
Slika 11. Spekter EXAFS kovinskega kobalta, izmerjen s sinhrotronsko svetlobo.

Signal EXAFS je periodičen v prostoru valovnega vektorja fotoelektrona k, v katerega ga pretvorimo iz energijske skale po enačbi (1.3). Rezultat je prikazan na sliki 11. Opazimo lahko, da amplituda oscilacij postopoma zamre pri večjih vrednostih valovnega vektorja. Kriterij, po katerem se odločimo, kako širok interval meritev lahko uporabimo pri nadaljnji analizi, je razmerje signal-šum. Za obdelavo pride v poštev samo tisti del spektra χ(k), v katerem je amplituda oscilacij EXAFS znantno večja od nivoja šuma.

Pri sinhrotronski meritvi je statistični šum običajno zelo nizek , ker je sinhrotron izjemno svetel izvir rentgenske svetlobe, tako da lahko analiziramo oscilacije EXAFS do k = 16 Å ali celo dlje. Pri meritvi z rentgensko cevjo pa je to zelo težko doseči, saj naraste potrebni čas za meritve preko vsake smiselne meje. V času, predvidenem za izvedbo meritve (8 ur), je mogoče izmeriti absorbcijski spekter kobaltove kovinske folije z razmerjem signal-šum, ki omogoča analizo spektra EXAFS do k ~ 13 Å.

 

Primerjava meritev z modelom EXAFS

Kovinski kobalt se v naravi pojavlja v kristalnih strukturah fcc ter hcp. V prvih dveh sosedskih lupinah imajo kobaltovi atomi v obeh kristalnih strukturah enako število atomov, v nadaljnjih lupinah pa se strukturi razlikujeta (tabela 2). Četrta in šesta lupina pri kristalni strukturi hcp se nahajata na enaki razdalji kot tretja in četrta lupina v strukturi fcc, vendar vsebujeta manjše število atomov. Poleg omenjenih lupin pa ima struktura hcp še dve dodatni lupini pri razdaljah, ki se ne ujemajo z nobeno lupino iz strukture fcc.

Tabela 2: Seznam razdalj koordinatnih lupin do razdalje 5,03Å ter število atomov v posamezni lupini za kovinski kobalt s kristalno strukturo fcc (a=3,55Å) in hcp (a=2,51Å, c=4,07Å) [28]. Kristalografski podatki za obe strukturi so določeni s pomočjo difrakcije.

fcc lupuna razdalja [Å] št. atomov 1 2,51 12 2 3,55 6 3 4,35 24 4 5,03 12

hcp lupina razdalja [Å] št. atomov 1 2,51 12 2 3,55 6 3 4,07 2 4 4,35 18 5 4,81 12 6 5,03 6

Na sliki 12 sta prikazani absolutni vrednosti Fourierovih transormirank modelskih spektrov EXAFS za obe strukturi. Modela upoštevata le prispevke sosedov na razdaljah, manjših od 6 Å od centralnega atoma. Prvi in največji vrh, ki pripada prvi lupini dvanajstih sosedov, je v obeh spektrih enak. Razlike pa so lepo opazne pri nadaljnjih vrhovih, ki jih prispevajo bolj oddaljene lupine.

Iz izmerjenega spektra EXAFS na kovinskem lističu kobalta je torej mogoče prepoznati kristalno strukturo vzorca tudi brez kvantitativne analize, kar s kvalitativno primerjavo FT izmerjenega spektra z obema modelskima spektroma s slike 12 na intervalu R med 3 Å in 6 Å.

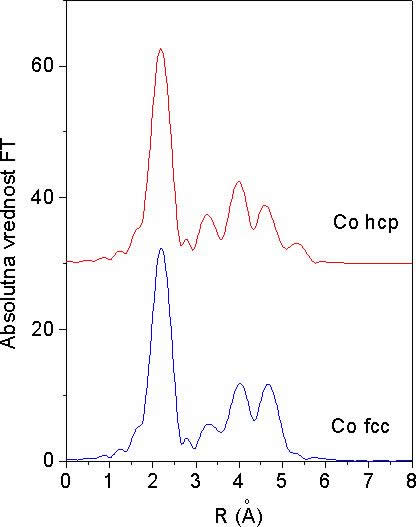
Slika 12. Absolutna vrednost Fourierove transformiranke modelskih spektrov EXAFS, za primer kobalta s kristalno strukturo fcc in hcp. Fourierova transformacija je izračunana z uteženjem spektra EXAFS s k na intervalu k = 4.5 Ǻ .. 13.0 Ǻ . V obeh modelih so upoštevani samo prispevki sosedov, ki so oddaljeni od centralnega atoma manj kot 6 Ǻ. Spektra sta zaradi preglednosti razmaknjena v vertikalni smeri.

 

OSNOVNI PRINCIPI MODELIRANJA SPEKTROV EXAFS

Modelna funkcija

Modelno funkcijo, ki jo bomo prilagajali izmerjenemu spektru EXAFS sestavimo iz prispevkov različnih sipalnih poti fotoelektrona. V primeru, ko se fotoelektron siplje le na enem izmed sosednjih atomov, imenujemo tako sipalno pot enojna sipalna pot (ESP). Če pa se fotoelektronski val siplje na sosedih večkrat, imenujemo tako pot večkratna sipalna pot (VSP). Podaljšana drobna struktura vsebuje prispevke obeh vrst poti:  

(5.3)

vsak izmed prispevkov pa je podan z:    

(5.4)

(5.5)

kjer je 2r dolžina sipalne poti.

Sipalno amplitudo f(k) in fazni premik (k) zaradi vpliva atomskih potencialov na fotoelektronski val izračunamo 'ab initio' za vsako izmed sipalnih poti posebej s programskim paketom FEFF6 [19]. Iz vhodnih podatkov program FEFF6 prebere koordinate posameznih atomov v kristalni mreži, ter nato izračuna vse možne sipalne poti z začetkom v izbranem atomu ter njihove degeneracije. Za izračun sipalne amplitude ter faznega premika upošteva medatomski potencial v kristalu, izračunan v približku 'muffin tin'.

V primeru, ko so na atom vezani atomi drugih vrst, povzročijo ti tako imenovani kemijski premik energije vezanih elektronov. Energija roba K se v takem primeru premakne za nekaj eV. Ta premik v modelni funkciji opišemo s parametrom premika ničelne energije fotoelektrona . Omenjeni parameter ne smemo fiksirati, ker z njim istočasno popravimo napako, ki je posledica uporabe medatomskega potenciala v približku 'muffin tin'. Premik ničelne energije fotoelektrona v gornjih dveh enačbah ni eksplicitno izražen, vključen pa je v valovnem vektorju kot:

(5.6)

Amplitudni faktor opiše zmanjšanje amplitude zaradi večkratnih vzbuditev v atomu ob fotoefektu v notranji lupini [20,21]. Vrednost za amplitudni faktor se giblje tipično med 0,8 do 0,9. Oba omenjena parametra sta skupna vsem sipalnim potem. Parametri, ki so lastni posameznim sipalnim potem, pa so število sosedov N, razdalja do sosedov rter DW faktor .

Vse parametre lahko zapišemo kot vektor , modelno funkcijo pa kot . V praksi moramo pri kristalnih strukturah upoštevati tudi do 100 različnih sipalnih poti, kar bi pomenilo, da bi morali upoštevati več kot 300 parametrov, to pa je očitno preveč. Preden lahko začnemo s prilagajanjem modelne funkcije, je torej potrebno zmanjšati število prostih parametrov.

Parameter, ki opisuje dolžino poti, lahko spreminjamo za vse sipalne poti hkrati, če vpeljemo relativno odstopanje mrežne razdalje () od vrednosti iz kristalografije d. Če spremenimo mrežno razdaljo, se celoten kristal napihne oziroma skrči, z njim pa se sorazmerno podaljša oziroma skrajša katerakoli sipalna pot:   

(5.7)

Enako vpeljemo za DW faktorje enoten model za vse sipalne poti v kristalu. Enačba (2.7) velja le za sipalno pot, ki vključuje dva sipalca. V splošnem velja za efektivni kvadrat odmika dolžine sipalne poti:     

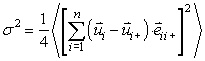(5.8)

kjer je n število atomov, ki jih vključuje sipalna pot,  je vektor odmika atoma i iz ravnovesne lege, i+ = i+1,  pa je enotski vektor, ki kaže v smeri od atoma i proti atomu i+ [18]. Vsak člen enačbe (5.8) izračunamo po enačbi ki jo daje korelirani Debyev model [22]:

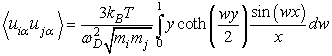(5.9)

kjer so , ,  pa številska gostota atomov; , kjer sta T temperatura kristala in Debyeva temperatura; =/, pa je Debyeva frekvenca, ki je definirana kot . Korelirani Debyev model upošteva gostoto stanj, ki jo daje Debyev model, poleg nje pa predpostavlja, da so v kristalu večinoma nihanja z valovnimi dolžinami veliko večjimi od najmanjših medatomskih razdalj. Posledica tega je, da sosednji atomi nihajo skoraj v fazi, bolj oddaljeni pa ne.

Za DW faktorje vseh sipalnih poti smo tako vpeljali dvoparametrično funkcijo temperature vzorca T in Debyeve temperature . Variacijski parameter je , dobljene rezultate za njegovo vrednost pa lahko po prilagajanju primerjamo s tabelirano vrednostjo za posamezno snov z dano kristalno strukturo.

Število sosedov v posamezni lupini je za kristalno strukturo znano. Pri modeliranju spektra EXAFS kovinske folije lahko degeneracije sipalnih poti enolično določimo in teh parametrov ne variramo. Pri skupkih pa povprečnega števila sosedov v posamezni koordinatni lupini ne poznamo. Tako ne poznamo degeneracij za posamezne sipalne poti, niti povezave med njimi. Število parametrov modelne funkcije želimo zmanjšati na tak način, da poiščemo povezavo med degeneracijami večkratnih sipalnih poti z degeneracijami enojnih sipalnih poti. V preteklosti so nekateri že poskušali s tako povezavo [11], vendar le za majhno število najkrajših sipalnih poti.

 

Numerično prilagajanje meritvam

Modelno funkcijo prilagodimo izmerjenemu spektru EXAFS z metodo najmanjših kvadratov. Vrednosti za parametre  dobimo, če z metodo najmanjših kvadratov s pomočjo Levenberg-Marquardtovega algoritma minimiziramo funkcijo:   

(5.10)

Čeprav je lahko podaljšana drobna struktura izmerjena v več tisoč točkah, to ne pomeni, da imamo pri prilagajanju ravno toliko neodvisnih točk. Podaljšana drobna struktura je sestavljena iz več sinusnih signalov. Če želimo v podaljšani drobni strukturi ločiti med dvema sinusnima členoma, s periodama, ki se razlikujeta za ,moramo meritev izvesti na območju k, da velja:      

(5.11)

kjer je uporabljen faktor 2, ker je perioda sinusnih členov v podaljšani drobni strukturi enaka 2r. Na enak način lahko zaključimo, da lahko v eni meritvi izmerjeni na intervalu k med seboj ločimo m sinusnih valov s periodami v intervalu r, kjer je:

(5.12)

Vrednost m je ocena za število neodvisnih točk prilagajanja [19].

Najpogosteje uporabljan kriterij za oceno kvalitete rezultatov prilagajanja je kriterij , ki ga izračunamo kot:   

(5.13)

kjer je k posamezna točka meritve, n je število vseh točk, pa je ocenjena napaka meritve, ki jo lahko v grobem ocenimo iz fotonske statistike. Če z detektorjem zabeležimo N sunkov, je napaka meritve: 

(5.14)

Za medsebojno primerjanje prilagajanj izvedenih na različno velikih intervalih in z različnimi parametri uporabimo reduciran hi kvadrat , ki je normiran s številom prostostnih stopenj pri prilagajanju , kjer je nvar število variacijskih parametrov oziroma dimenzija vektorja :        

(5.15)

Klasičen postopek za oceno napake parametrov izvira iz predpostavke, da so statistične napake meritev porazdeljene po normalni distribuciji in ne vsebujejo sistematičnih napak. V takem primeru je okvirna vrednost kriterija . V resnici modelna funkcija ni popolnoma pravilna. Ocenjeno je, da lahko podaljšano drobno strukturo opiše do 1% natančno, zato se tolerirajo tudi vrednosti .

Za izračun napake posameznih variacijskih parametrov in njihove medsebojne korelacije potrebujemo matriko ukrivljenosti prostora [23]:

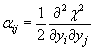(5.16)

Njeno inverzno matriko imenujemo korelacijska matrika . Napake parametrov so določene z diagonalnimi členi inverzne korelacijske matrike, korelacije med parametri pa z nediagonalnimi členi:      

(5.17)

(5.18)

Napake parametrov lahko tudi grafično prikažemo na večdimenzionalnem grafu (slika 5.1), katerega osi predstavljajo parametre . Če povežemo vse točke na grafu, v katerih je vrednost za 1 večja od najmanjše dobimo večdimenzionalni elipsoid s središčem v točki, katere koordinate predstavljajo optimalne vrednosti parametrov. Če točke elipsoida projiciramo na posamezno os, nam razdalja od središča elipsoida do najbolj oddaljene projekcije predstavlja napako posameznega parametra .

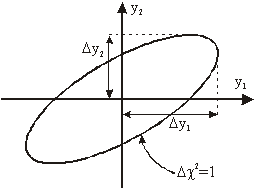
Slika 5.1: Grafični prikaz napak parametrov prilagajanja v prostoru z dvema parametroma .

Če hočemo določiti realno napako za posamezne variacijske parametre oziroma korelacije med njimi potrebujemo dobro oceno za napako meritve. Napako, ki je posledica statistike smo že ocenili, za sistematično napako pa nimamo nobene ocene. Za oceno napak parametrov potrebujemo celotno napako meritve, ki vsebuje tudi del sistematične napake. Standardni postopek za oceno celotne napake temelji na predpostavki, da bi veljalo =1 v primeru, če sistematične napake ne bi bilo [19]. Ker je sistematična napaka vedno različna od nič, je tudi >1, celotno napako pa lahko izračunamo kot:    

(5.19)

To vrednost uporabimo pri izračunu resničnih napak parametrov in njihovih medsebojnih korelacij.

 

KATEGORIZACIJA VEČKRATNIH SIPALNIH POTI

Zaradi velikega števila večkratnih sipalnih poti, je za njih najprej potrebno izbrati enoličen zapis. Zapišemo jih na naslednji način:                                                  
                             .
Sipalni atomi, ki so v našem primeru vedno kobaltovi atomi, so med seboj povezani s puščicami, ki nakazujejo vrstni red sipalcev. Oznaka nad puščico (a,b,c,…,z) označuje razdaljo med dvema zaporednima sipalcema. Dolžina vsake poti je tako enaka:                

(6.1)

Indeks nad oznako sipalca (x,y,…) označuje njegovo oddaljenost od centralnega atoma (Co), v oklepajih pa je naveden sipalni kot pod katerim se siplje fotoelektron. Vsaka sipalna pot se zaključi s centralnim atomom.

Vse sipalne poti lahko razporedimo v 4 družine. V primeru sipalne poti, ko fotoelektron potuje le do enega sosednjega atoma ter nazaj, tako pot uvrstimo v družino enojnih sipalnih poti (ESP) (slika 6.1). V primeru, ko sipalna pot vključuje dvakrat ponovljeno ESP, jo uvrstimo v družino dvakratnih sipalnih poti (DSP) (slika 6.1). Te dve družini obsegata vse sipalne poti, ki vključujejo le po dva sipalna atoma. Znotraj družine se sipalne poti razlikujejo po razdalji med obema atomoma, ki jo za označevanje dodamo ob oznako družine (ESPa, DSPa). Celoten zapis obeh poti je torej:     
ESPa:   ,       
DSPa:   .

         

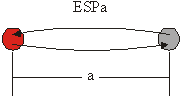
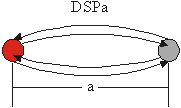
Slika 6.1: Shematski prikaz sipalne poti enojnega sipanja ESPa in dvakratnega sipanja DSPa, kjer a označuje razdaljo med obema atomoma v enotah najbližjih sosedov. Centralni atom je obarvan rdeče.

Tretja družina obsega sipalne poti s tremi sipalci, ki ležijo na isti premici. Razdalja med prvim in drugim atomom je enaka razdalji med drugim in tretjim atomom. Ker so vsi sipalni koti enaki bodisi 0° bodisi 180° imenujemo to družino družina linearnih sipalnih poti (LSP). Med seboj se sipalne poti znotraj te družine razlikujejo po razdalji med dvema sosednjima sipalcema (a/2) ter po številu sipanj in položaju centralnega atoma, kar označimo z indeksno številko nad oznako družine (slika 6.2).

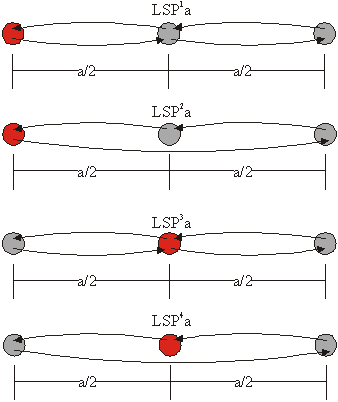
Slika 6.2: Shematski prikaz sipalnih poti linearnih sipanj LSPa – LSPa, kjer a označuje polovično dolžino sipalne poti. Centralni atom je obarvan rdeče.

Linearne sipalne poti zapišemo kot:        
LSP1a:   ,                      
LSP2a:   ,                                                  
LSP3a:   ,                       
LSP4a:   .

Naslednja družina obsega sipalne poti, ki vključujejo tri sipalne atome, ki ne ležijo na isti premici. Sipalni atomi so postavljeni v oglišča trikotnika s stranicami a,b,c in notranjimi koti , zato poimenujemo to družino družina trikotnih sipalnih poti (TSP). Posamezne sipalne poti v tej družini se med seboj razlikujejo po dolžini stranic trikotnika (a,b,c) in načinu sipanja med atomi, kar označimo z indeksom nad oznako družine (slika 6.3).

Enolično lahko zapišemo trikotne sipalne poti kot        
TSP1abc:   ,  
TSP2abc:   ,             
TSP3abc:  

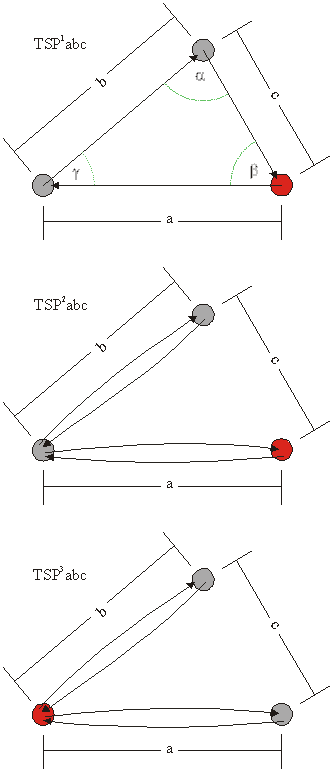
Slika 6.3: Shematski prikaz trikotnih sipalnih poti TSPabc, TSPabc in TSPabc, kjer a,b,c označujejo razdaljo med dvema zaporednima atomoma. Centralni atom je obarvan rdeče.

 

ANALIZA MERITEV

Programska oprema

Za analizo absorpcijskih spektrov EXAFS smo uporabili programski paket IFEFFIT [15], ki združuje več samostojnih paketov. Podaljšano drobno strukturo izluščimo iz izmerjenega absorpcijskega spektra s programom ATHENA [9]. Ko pripravimo (k) lahko s programom FEFF izračunamo fazni premik (k) in sipalno amplitudo f(k) za vsako izmed sipalnih poti. Kot vhodne podatke uporabimo koordinate ter vrsto atomov, ki obkrožajo centralni atom. V primeru pravilnih kristalnih struktur nam razpored atomov okoli izbranega centralnega atoma izračuna program ATOMS [9] iz znanih kristalografskih podatkov. Izmerjeni podaljšani strukturi prilagajamo modelno funkcijo v prostoru r s programom ARTEMIS [9].

 

Kristalna struktura kovinskega kobalta

Kovinski kobalt se v naravi nahaja v dveh kristalnih strukturah fcc ( -Co) in hcp ( -Co).Pri meritvah smo imeli vzorec kovinskega kobalta s strukturo fcc [12].

Najprej moramo raziskati, katere sipalne poti ustrezajo določenim lupinam. V modelno funkcijo vključimo sipalne poti, ki sestavljajo prve štiri koordinatne lupine (slika 13). V modelno funkcijo strukture fcc smo tako vključili 5 enojnih in 39 večkratnih sipalnih poti, od katerih je 5 poti kolinearnih, s polovičnimi dolžinami manjšimi od 6.3 Å.

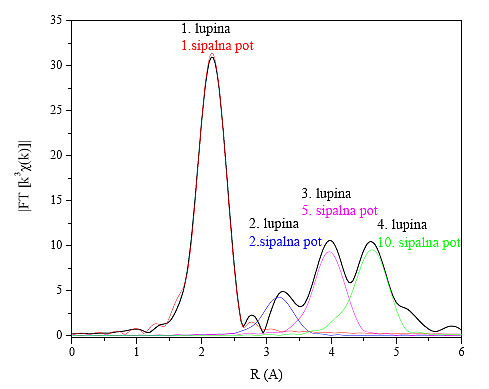
Slika 13 : Absolutna vrednost Fourierove transformiranke podaljšane drobne strukture kovinskega kobalta s kristalno strukturo fcc (črno). V barvah so prikazani glavni prispevki sipalnih poti, ki so vključeni v modelno funkcijo.

Začnemo z modelno funkcijo, ki opiše samo prvo lupino. Za prilagajanje v prostoru r izberemo območje, do koder prva lupina sega, to je 1.65 Å< r < 2.77 Å. Signale na območju pod 1.65 Å izpustimo, saj ti ne morejo biti prispevki sipanja fotoelektrona na atomih, ker so to razdalje manjše od kakršnekoli medatomske razdalje.

V prostoru k izberemo področje prilagajanja 2 Å < k < 16 Å in ga ne spreminjamo, ko posamezne sipalne poti postopoma dodajamo. V prostoru k smo navzdol omejeni z metodo EXAFS, ki pod spodnjo mejo meritev ne opiše dobro. Pri višjih vrednostih k pa amplituda EXAFS pojema, zato je zgornja meja primernega področja izbrana do take vrednosti, kjer je amplituda signala še večja od šuma.

Na začetnem izbranem območju r in k prve lupine v modelno funkcijo vključimo samo prvo sipalno pot. Prosti parametri so amplitudni faktor , premik ničelne energije fotoelektrona , relativno odstopanje mrežne razdalje (d/d) od kristalografske vrednosti, ter povprečni kvadrat odmika razdalje . Izračunanih vrednosti za , (d/d) ter , ki jih dobimo pri modeliranju prve lupine, pri modeliranju nadaljnih lupin ne spreminjamo več.

V naslednjem koraku vključimo še vse preostale sipalne poti. Modelni funkciji v prostoru r razširimo na interval 1.65 Å < r < 6 Å. DW faktorje vseh sipalnih poti modeliramo z Debyevim modelom, v katerem je prost parameter Debyeva temperatura . Relativne degeneracije vseh sipalnih poti N fiksiramo, saj kristalografsko strukturo poznamo, variiramo pa amplitudni faktor .

Najboljše vrednosti izračunanih parametrov so navedene v tabeli 3. Na izbranem območju imamo na voljo 30 neodvisnih točk, kar je dovolj za 5 prostih parametrov.

					[Å]	[K]		R
Co - fcc	0.77(1)	0.4(4)	0.053(2)	0.0156(4)	0.0068(2)	362(5)	10	0.0074

Tabela 3 : Dobljene vrednosti parametrov, ki smo jih dobili s prilagajanjem modela fcc: amplitudni faktor, premik ničelne energije fotoelektrona, (d/d)1 relativna napaka mrežne razdalje glede na kristalografsko za prvo lupino, (d/d) pa še za preostale lupine, povprečni kvadrat odmika razdalje za prvo lupino, Debyeva temperatura. Na koncu vrednosti parametrov so v oklepajih podane napake na zadnji decimalki.

Izračunane vrednosti parametrov potrjujejo kristalno strukturo fcc kovinskega kobalta. Relativno odstopanje mrežne razdalje od kristalografskih podatkov znaša d/d = 1.6%. V literaturi [20] je za kovinski kobalt tabelirana Debyeva temperatura = 385 K, od katere se dobljena vrednost z modelom fcc razlikuje le za 6%.

Na sliki 15 je prikazana absolutna vrednost Fourierove transformiranke izmerjenega spektra EXAFS, ki je prikazan na predhodnji sliki 14, ter model kristalne strukture fcc.

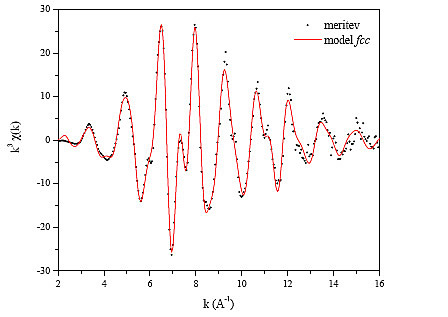
Slika 14 : Spekter EXAFS nad absorpcijskim robom K, izmerjen na kobaltovi kovinski foliji. Pike - meritev, polna (rdeča) črta - model kristalne strukture fcc.

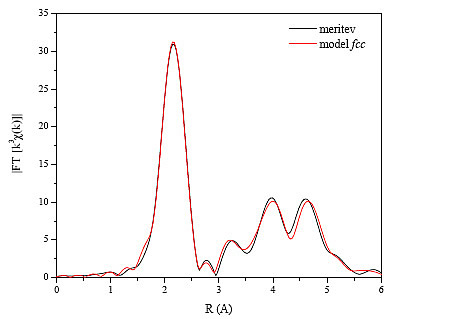
Slika 15 : Absolutna vrednost Fourierove transformiranke Co spektra EXAFS, ki je prikazan na sliki 14. Črna črta - meritev; rdeča črta - modelska funkcija kristalne strukture fcc.

 

Opombe

7. Meritev je bila izvedena na žarkovni liniji E4,v katero je vgrajeno toroidno zrcalo z zlato prevleko, ki zbere rahlo divergentni sinhrotronski žarek na mestu vzorca, ter dvokristalni Braggov monokromator Si(111), ki monokromatizira belo rentgensko svetlobe z energijsko ločljivostjo 1 eV. Jakost vpadne in prepuščene svetlobe merita ionizacijski celici, napolnjenimi z dušikom. Sinhrotron je izjemno svetel izvir rentgenske svetlobe, zato je čas meritve relativno kratek: tipično 1s/kanal ozirma ~30 minut/spekter.

 

E-mail:iztok.arcon@p-ng.si Last change: 07-Jun-2006