EXAFS

NANO SKUPKI

 

KOBALTOVI SKUPKI

MERITVE

Priprava vzorcev

Z metodo EXAFS sem analiziral kobaltove skupke, vgrajene v silikatno matriko. Ta material ima katalitske lastnosti, tako se katalizatorji, ki vsebujejo kobalt, uporabljajo za katalizo pri Fischer-Tropschevi reakciji, kjer sodelujejo pri hidrogenaciji ogljikovega monoksida v alifatske ogljikovodike [2].

Proučeval sem tri različne vzorce kovinskih kobaltovih skupkov. Dva od njih (Co-1, Co-2) sta bila pripravljena z amoniakovo metodo [24,
25], pri kateri najprej pripravijo raztopino kobaltovih nitratov v argonovi atmosferi, da jo zavarujejo pred zrakom. Med mešanjem dodajajo 22% raztopino amoniaka in nato mikroporozni silikat (200 m/g). Vzorec centrifugirajo,  izperejo in posušijo v vakuumu pri 353 K. Prekurzor 8 ur reducirajo z vodikom, vzorec medtem segrevajo 1,3 K/min do temperature 923 K, pri kateri ga zadržijo še za 2 uri. Vzorca se med seboj razlikujeta po končnih masnih deležih kobalta v silikatni mreži: 17,6% in 3,2%.

Tretji vzorec (Co-3) je bil pripravljen s fluoridovo metodo [26]. Raztopini kobaltovega fluorida segrejejo na 333 K za 30 minut. Vzorcu dodajo mikroporozni silikat (800 m/g) in mešajo pri isti temperaturi 2 uri. Trdno snov vzorca posušijo v vakuumu pri 393 K. Prekurzor reducirajo z vodikom pri segrevanju vzorca 1,3 K/min do temperature 1023 K. Končni masni delež kobalta v vzorcu je 1,83%.

Med procesom redukcije nastajajo na površini silikatne mreže iz kobaltovih nitratov majhni kovinski skupki kobalta. Velikost in oblika nastalih skupkov je neznana, rast skupkov pa omejujejo razvejane strukture silikatne matrike. Struktura silikatne matrike je neurejena, zaradi tega nimamo podatkov po katerih bi lahko sklepali na velikost in obliko nastalih skupkov.

 

Opis meritev EXSAFS

Absorpcijski spektri kobaltovih vzorcev v energijskem področju nad robom K so bili posneti v sinhrotronskem laboratoriju Hasylab v Desy na postaji EXAFS II. Vpadni curek rentgenske sinhrotronske svetlobe fokusira pozlačeno toroidno zrcalo, energijo fotonov pa izberemo z dvokristalnim silicijevim monokromatorjem Si(111), ki ga vodimo s koračnimi motorji. Z dvema ionizacijskima celicama merimo jakost vpadnega in prepuščenega curka po prehodu skozi vzorec. Signale vodimo na večkanalni analizator, od koder jih preberemo z računalnikom za nadaljnjo obdelavo. V curku, ki izhaja iz monokromatorja, so fotoni, za katere je izpolnjen Braggov pogoj za sipanje na kristalnih ravninah              

(8.1)

Višje rede sipanja (n=2,3,…) odpravimo z rahlim zasukom drugega kristala iz paralelne lege. S povratno zanko na tak način tudi vzdržujemo konstantni vpadni tok svetlobe.

Energijska ločljivost je odvisna od zaslonke pred monokromatorjem, s katero izberemo le fotone, ki se sipljejo pod kotom

V energijskem področju kobaltovega roba K je bila energijska ločljivost 1,5eV [27]. Za primerjavo je bil poleg treh absorpcijskih spektrov kobaltovih skupkov posnet tudi absorpcijski spekter kovinskega kobalta (slika 8.1).

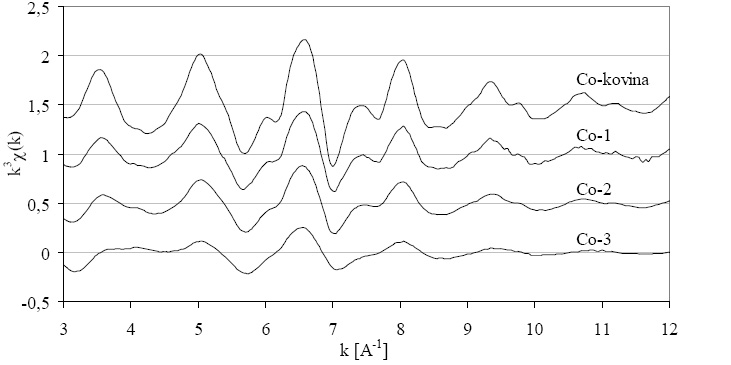
Slika 8.2: Podaljšane drobne strukture kovinskega kobalta in treh kobaltovih vzorcev nad kobaltovim robom K utežene s k.

 

ANALIZA MERITEV

Za analizo absorpcijskih spektrov EXAFS smo uporabili programski paket UWXAFS [19], ki združuje več samostojnih paketov. Program FEFF6 izračuna fazni premik(k) in sipalno amplitudo f (k) za vsako izmed sipalnih poti. Kot vhodne podatke uporabi koordinate ter vrsto atomov, ki obkrožajo centralni atom. V primeru pravilnih kristalnih struktur nam vhodne podatke izračuna program ATOMS. Podaljšano drobno strukturo izluščimo iz izmerjenega absorpcijskega spektra s programom AUTOBK. Izmerjeni podaljšani strukturi prilagajamo modelno funkcijo (5.3, 5.4, 5.5) v prostoru r s programom FEFFIT. Postopek prilagajanja je podrobneje opisan na strani analiza.

Kristalna struktura kovinskega kobalta

Najprej se lotimo določanja kristalne strukture kovinskega vzorca. Ko prepoznamo njegovo kristalno strukturo, lahko s prilagajanjem modelne funkcije meritvam narejenim na tem vzorcu preverimo natančnost metode pri strukturni analizi. Rezultati prilagajanja na znani strukturi so uporabni za normiranje metode.

fcc lupina razdalja [Å] št. atomov 1 2,51 12 2 3,55 6 3 4,35 24 4 5,03 12

hcp lupina razdalja [Å] št. atomov 1 2,51 12 2 3,55 6 3 4,07 2 4 4,35 18 5 4,81 12 6 5,03 6

Tabela 9.1: Seznam razdalj koordinatnih lupin do razdalje 5,03Å ter število atomov v posamezni lupini za kovinski kobalt s kristalno strukturo fcc (a=3,55Å) in hcp (a=2,51Å, c=4,07Å) [28]. Kristalografski podatki za obe strukturi so določeni s pomočjo difrakcije.

Kovinski kobalt se v naravi pojavlja v kristalnih strukturah fcc ter hcp [28]. V prvih dveh koordinatnih lupinah imata obe kristalni strukturi enako število atomov, v nadaljnjih lupinah pa se strukturi razlikujeta (tabela 9.1). Četrta in šesta lupina pri kristalni strukturi hcp se nahajata na enaki razdalji kot tretja in četrta lupina v strukturi fcc, če pa primerjamo število atomov v ujemajočih lupinah med obema strukturama, ugotovimo, da je število atomov manjše pri strukturi hcp. Poleg omenjenih lupin pa ima struktura hcp še dve lupini pri razdaljah, ki se ne ujemajo z nobeno lupino iz strukture fcc.

Modelno funkcijo za strukturo fcc sestavimo iz prispevkov sipalnih poti na prvih štirih koordinatnih lupinah. Upoštevamo štiri enojne in 22 večkratnih sipalnih poti s polovično dolžino manjšo od 5,2Å. Pri hcp modelu pa upoštevamo prvih 6 enojnih ter 19 večkratnih sipalnih poti s polovičnimi dolžinami manjšimi od 5,2Å. Če bi hoteli analizirati še bolj oddaljene lupine na primer do razdalje 8,2Å, bi število ustreznih sipalnih poti naraslo nad 150, kar je preveč za zmogljivosti programskega paketa [19], ki sem ga uporabljal. Program lahko vključi do 100 sipalnih poti.

Signali z ustreznimi razdaljami pod 1,2Å ne morejo biti prispevki sipanja na sosedih, saj je taka razdalja premajhna za kakršnokoli medatomsko razdaljo. Ti signali so v resnici dolgovalovni ostanki ozadja, ki se jih ne da opisati z zlepkom polinomov. Pri prilagajanju jih seveda ne smemo upoštevati, zato izberemo za prilagajanje v prostoru r območje 1,2Å< r <5,2Å. V prostoru k smo izbrali področje prilagajanja 4Å< k <13Å. V tem prostoru smo navzdol omejeni z metodo EXAFS, ki pod spodnjo mejo meritev ne opiše dobro. Pri višjih vrednostih k pa amplituda EXAFS pojema, zato je zgornja meja primernega področja izbrana pri taki vrednosti, kjer je amplituda signala še večja od šuma.

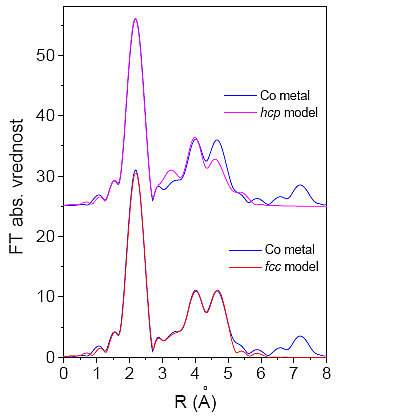
Slika 9.1: Primerjava izmerjenega spektraEXAFS z modelom fcc in modelom hcp.

Na izbranem območju prilagajamo izmerjenim podatkom modelirani funkciji za kristalni strukturi fcc in hcp (slika 9.1). Relativne degeneracije sipalnih poti so fiksirane, prosti parametri pa so amplitudni faktor, premik ničelne energije fotoelektrona , relativno odstopanje mrežne razdalje d/d od kristalografske vrednosti, in. Na tem mestu je potrebno poudariti, da smo za izračun DW faktorja prve lupineuporabili neodvisen prost parameter (2.6), za vse ostale lupine pa smo DW faktorje modelirali z Debyevim modelom (5,9), v katerem je bil prost parameter Debyeva temperatura. Najboljše vrednosti parametrov so navedene v tabeli 9.2. Na izbranem območju imamo na voljo 24 neodvisnih točk (5.12), kar je povsem dovolj za 5 prostih parametrov.

model		d/d	[eV]	[Å]	[K]
fcc	0,86(7)	0,011(1)	4(1)	0,0070(6)	363(10)	200
hcp	0,92(9)	0,001(3)	4,8(4)	0,0074(7)	410(30)	300

Tabela 9.2: Najboljše vrednosti parametrov dobljene s prilagajanjem modelov fcc in hcp. Napaka na zadnji decimalki je podana zraven vrednosti v oklepajih.

Ugotovimo, da se model fcc dobro ujema z meritvami. Dobljeno relativno odstopanje mrežne razdalje od kristalografskih podatkov [28] znaša d/d=1,1%. Tudi Debyeva temperatura pri sobni temperaturi se ujema s podatki iz literature za fcc kristalno strukturo = 365K [28]. Model hcp pa ne more ustrezno popisati izmerjenega spektra. Po pričakovanjih je ujemanje dobro pri signalu prve lupine, saj je ta lupina enaka za oba modela, razlike pa se opazijo pri nadaljnjih lupinah. Na sliki 9.1 je razvidno, da model hcp ne more dobro opisati drugega in četrtega vrha, od tod vidimo, da oba modela lahko med seboj ločimo šele, ko upoštevamo tudi višje koordinatne lupine. Če primerjamo vrednosti kriterija za obe strukturi, lahko ponovno zaključimo, da se model s kristalno strukturo fcc veliko bolje ujema z meritvijo kovinskega vzorca kot pa model s kristalno strukturo hcp.

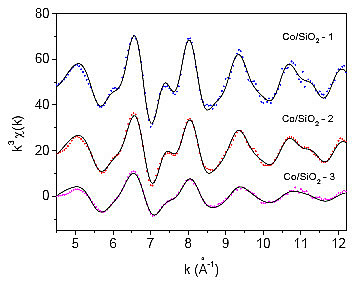
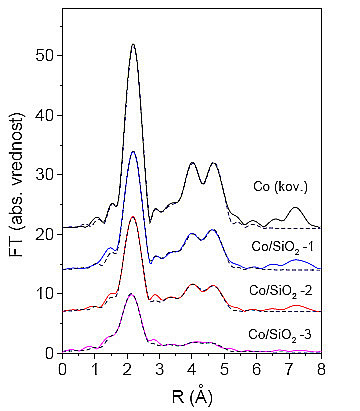
Slika 9.2 (a): Spektri EXAFS izmerjeni na kobaltovih skupkih v silikatni matriki Co/SiO: pike -meritev; polna črta –model EXAFS (fcc).	Slika 9.2 (b): Fourierove transformiranke spektrov EXAFS kobaltovih skupkov. Za primerjavo je prikazan tudi spekter kovinskega kobalta. Polna črta-meritev; črtkano –model EXAFS (fcc).

V našem primeru prilagajanja z znano kristalno strukturo fcc, smo dobili relativno veliko vrednost za faktor=200. Največ je k temu prispevalo neujemanje v območjučetrtega vrha, kjer v modelni funkciji manjkajo prispevki repov višjih sipalnih poti. Vrednost = 0,86, ki smo jo dobili s tem prilagajanjem za amplitudni faktor uporabimo pri analizi Co skupkov in je ne variiramo.

Iz absolutnih vrednosti FT izmerjenih podaljšanih drobnih struktur vseh vzorcev s Co skupki lahko kar takoj vidimo, da imamo opravka s tremi različnimi vzorci (slika 9.2), saj se posamezni vrhovi med vzorci razlikujejo po svoji višini. Že sedaj lahko domnevamo, sodeč po enako visokih tretjem in četrtem vrhu, da imajo vsi trije vzorci kristalno strukturo fcc. V primeru kristalne strukture hcp je namreč četrti vrh znatno nižji od tretjega (slika 9.1). Analizo podaljšanih drobnih struktur kobaltovih skupkov bomo izvajali postopoma, začenši z analizo prvega vrha, nato pa bomo poskušali analizirati vse vrhove do 5Å.

 

Analiza signala prve lupine sosedov

Najprej si oglejmo rezultate prilagajanja na prvem vrhu. Prilagajamo na območju 1,2Å< r<2,6Å, v k prostoru pa ostane območje enako kot v primeru kovine, 4Å< k <13Å. Tako območje v k prostoru bomo uporabili tudi v vseh nadaljnjih analizah, zato to ne bo več posebej navedeno. Za prilagajanje imamo na voljo 8 neodvisnih točk za 4 spremenljive parametre , d/d, , . Rezultati za tri vzorce skupkov in referenčni rezultati za kovino so navedeni v tabeli 9.3.

Vzorec		[Å]	d/d	(eV)
Co-kovina	1,00(3)	0,0069(2)	0,0043(8)	6,0(5)	28
Co-1	0,68(9)	0,0072(9)	0,003(3)	5(2)	31
Co-2	0,62(7)	0,0080(8)	0,001(3)	4(1)	470
Co-3	0,5(1)	0,011(2)	-0,02(2)	0(3)	180

Tabela 9.3: Rezultati prilagajanja na prvem vrhu za tri vzorce kobaltovih skupkov in kovinskega kobalta za primerjavo. Napaka na zadnji decimalki je podana zraven vrednosti v oklepajih.

Že iz takega najpreprostejšega prilagajanja dobimo nekatere zanimive ugotovitve. Vidimo lahko, da je delež sosedov v prvi lupini največji v vzorcu Co-1 in najmanjši v vzorcu Co-3, kar kaže na to, da ima vzorec Co-1 največje skupke, Co-3 pa najmanjše. Za kovinski vzorec smo dobili po pričakovanju rezultat 1. Povprečni kvadrat odmika dolžine sipalne poti predstavlja neurejenost strukture. Ta je najmanjša v kovinskem vzorcu, največja pa pri najmanjših skupkih. Zanimivi so tudi rezultati za relativno spremembo mrežne razdalje d/d. Opazimo, da je mrežna razdalja pri majhnih skupkih manjša od tiste pri velikih skupkih oziroma pri kovini, kar so pokazale že nekatere prejšnje raziskave [29].

Zaradi ožjega intervala v prostoru r so sedaj vrednosti pri kovini in pri vzorcih Co-1 in Co-3 pričakovano nižje, kot pri prilagajanju kovinskega spektra (tabela 9.2). Razlog je v tem, da smo tokrat prilagajali le na območju prvega vrha, ki ga model najbolje opiše, saj se ga da razmeroma dobro ločiti od prispevkov ostalih sipalnih poti. Kvaliteta prilagajanja pri zadnjih dveh vzorcih je veliko slabša kot pri vzorcih kovine in Co-1. Najverjetnejša razlaga za tako razliko je ta, da je model za zadnja dva skupka pomanjkljiv. Prilagajanje ponovimo z dodatno lupino kisikov pri razdalji 2Å. Taka Co-O razdalja je tipična za kobaltove okside [27,30,31].Predpostavka, s katero vpeljemo novo lupino kisikov, je ta, da je v zadnjih dveh vzorcih bodisi površina skupkov delno oksidirana bodisida so skupki v stiku s kisiki iz silikata. Prisotnost dodatne lupine kisikov preverimo tudi na vzorcu Co-1, prilagajanje z dodatno lupino kisikov pa ponovimo tudi pri vzorcu kovine, da preverimo stabilnost modela.

Analizo prvega vrha ponovimo na enakem območju v r prostoru z dodatno lupino kisika, ki jo prilagajamo z dvema novima spremenljivima parametroma , . Za kisik smo fiksirali povprečni kvadrat odmika razdalje na 0,004 Å, kar je tipična vrednost za Co-O koordinacijo v spojinah. [27, 30, 31]. Izkaže se, da ne moremo hkrati zanesljivo določiti in  saj je korelacija med njima prevelika. Kljub uvedbi novih parametrov imamo še vedno več neodvisnih točk kot spremenljivih parametrov. Rezultati prilagajanja so navedeni v tabeli 9.4.

Vzorec		[Å]	d/d	[eV]		[Å]
Co-kovina	0,98(4)	0,0069(3)	0,0048(8)	6,2(6)	0,3(3)	2,0(7)	40
Co-1	0,66(9)	0,007(1)	0,004(4)	5(2)	0,4(8)	2,0(7)	57
Co-2	0,59(6)	0,0078(7)	0,003(3)	5(1)	0,7(4)	2,0(7)	350
Co-3	0,47(9)	0,010(2)	0,00(8)	5(3)	1,1(6)	2,0(7)	130

Tabela 9.4: Rezultati prilagajanja na prvem vrhu za tri vzorce kobaltovih skupkov in kovinskega kobalta za primerjavo. Poleg signala prve lupine kobalta smo v tem primeru modelirali tudi lupino kisika. Napaka na zadnji decimalki je podana zraven vrednosti v oklepajih.

Rezultati parametrov ,in d/d so se od prejšnjega prilagajanja le malo spremenili. Vzorec Co-1 še vedno kaže na največje skupke, vzorec Co-3 pa na najmanjše. Podobno tudi spreminjanje parametrov in d/d glede na velikost skupkov ostaja enako kot v prejšnjem primeru. Pri dodatni lupini kisikov opazimo največje povprečno število kisikov v vzorcu z najmanjšimi skupki. To smo tudi pričakovali, saj smo predvidevali, da se kisikovi atomi vežejo le na površinske atome, delež takih atomov pa je ravno pri najmanjših skupkih največji. Kisike opazimo tudi v primeru kovinskega vzorca, kar pa ne pomeni, da je v kovinskem vzorcu prisoten tudi kisik. Dobljena vrednost 0,3 je preprosto najnižja meja natančnosti, s katero lahko z metodo EXAFS na naših vzorcih določimo število kisikov v taki koordinatni lupini. Upravičenost vpeljave nove koordinatne lupine kisikov lahko preverimo s primerjavo kriterija . Ta se je z uvedbo nove lupine zmanjšal le za vzorca Co-2 in Co-3, kar pomeni, da je le pri omenjenih dveh vzorcih smiselno upoštevati lupino kisikov.

 

Analiza nadaljnih lupin sosedov

Ko analiziramo tudi višje koordinatne lupine, sestavimo modelno funkcijo iz prispevkov prvih štirih enojnih sipalnih poti (ESP) (slika 6.1) ter 22 večkratnih sipalnih poti (VSP) (sliki 6.2 in 6.3). Poleg njih pa pri vzorcih Co-2 in Co-3 upoštevamo še prispevek kisikove koordinatne lupine pri razdalji 2Å. Za izračun DW faktorjev za vse poti razen za ESP1 in za sipalne poti, ki vključuje kisikove atome, uporabimo koreliran Debyev model (4.18), relativne degeneracije VSP pa vežemo na relativne degeneracije ESP po postopku, ki smo ga opisali v sedmem poglavju. (enačbe 7.1, 7.4 in 7.6). Modelirano funkcijo prilagajamo na področju 1,2Å< r <5,2Å, kar pomeni 24 neodvisnih točk, uporabimo pa 11 spremenljivih parametrov:,,,, , , , , ,  ter . Prvemu vrhu nismo dodelili nobenega variacijskega parametra skupnega z ostalimi vrhovi. S tem smo dosegli, da s prilagajanjem bolje opišemo tudi višje lupine, saj bi v nasprotnem primeru prvi vrh zaradi svoje velike amplitude sam narekoval rezultate prilagajanja. Rezultati prilagajanja so navedeni v tabeli 9.5.

Vzorec [Å] [K] Co-kovina 1,00(5)  0,9(1) 1,0(2) 1,07(9) 0,0069(4) 364(9) Co-1 0,68(8) 0,6(2) 0,6(2) 0,57(9) 0,0072(8) 370(20) Co-kovina +O 0,99(6) 0,9(2) 1,03(9) 1,07(9) 0,0069(4) 360(10) Co-2 +O 0,60(5) 0,5(2) 0,54(9) 0,51(9) 0,0079(6) 340(20) Co-3 +O 0,48(7) 0,8(9) 0,5(5) 0,5(5) 0,010(1) 250(60)

Vzorec [eV] [Å] Co-kovina 0,008(1) 0,009(3) 5,4(5) - - 66 Co-1 0,006(2) 0,005(6) 5(1) - - 23 Co-kovina +O 0,008(1) 0,009(3) 5,4(6) 0,0(3) 2(1) 75 Co-2 +O 0,007(2) 0,006(4) 5,2(9) 0,6(3) 1,98(3) 216 Co-3 +O 0,004(4) 0,00(1) 5(2) 1,2(3) 1,98(2) 40

Tabela 9.5: Rezultati prilagajanja na področju prvih štirih vrhov. Napaka na zadnji decimalki je podana zraven vrednosti v oklepajih. Dodatna koordinatna lupina kisikov je prisotna le pri vzorcih Co-2 in Co-3. Primerjava s kovino je narejena za primer brez kisikove lupine in z njo (oznaka +O). Spodnja tabela je nadaljevanje zgornje. Zgornja tabela ter prva dva stolpca v spodnji tabeli vsebujejo podatke o kobaltovih lupinah, ostali stolpci v spodnji tabeli pa podatke o dodani kisikovi lupini in kvaliteti prilagajanja.

Na tem mestu smo hkrati tudi prvič potrdili, da je predlagan način določanja relativnih degeneracij za večkratna sipanja ki smo ga vgradili v model, v resnici dober in učinkovit. Pri prilagajanju kovine smo po pričakovanjih dobili vrednosti deležev sosedov . Če uporabimo katerega izmed modelov [11], ki ne upošteva takšnega števila VSP, kot smo jih mi, so ti deleži signifikantno prerazporejeni, kar kaže na pomanjkljivo sestavljeno modelno funkcijo.

Odvisnosti, ki smo jih opazili v prejšnjih primerih prilagajanja na prvem vrhu, lahko opazimo tudi v tem primeru. Po deležih sosedov iz vsake izmed prvih štirih koordinatnih lupin vidimo, da vsebuje vzorec Co-1 največje, vzorec Co-3 pa najmanjše skupke. Edino odstopanje iz opisane odvisnosti opazimo pri deležu sosedov v drugi koordinatni lupini pri vzorcu Co-3, vendar pa je napaka tega parametra tako velika, da raje zaupamo deležem sosedov v ostalih koordinatnih lupinah. Pri deležih sosedov pri kovini vidimo, da ne dobimo točnih vrednosti 1, kot bi pričakovali, ampak majhna sistematična odstopanja, ki so posledica korelacij med parametri modela. Podobne korelacije pričakujemo tudi pri skupkih, zato uporabimo te vrednosti za normiranje rezultatov dobljenih na vzorcih skupkov.

Nered je še vedno največji pri najmanjših skupkih. To opazimo po parametru prvega vrha , kot tudi po Debyevi temperaturi, ki opisuje nered v vseh višjih sipalnih poteh. Debyeva temperatura je najnižja pri najmanjših skupkih in največja pri največjih,kar se sklada z že prej opaženo odvisnostjo od velikosti skupka, ki smo jo opazili na prvi lupini.

Relativno odstopanje mrežne razdalje od kristalografskih podatkov za kovino je pri najmanjših skupkih najmanjše, za razliko s prejšnjim prilagajanjem pa iz prej opažene odvisnosti izstopata vzorca Co-1 in Co-2. Vseeno pa odstopanje ni večje od napake, s katero je parameter določen. Za prvo koordinatno lupino smo uporabili poseben parameter za relativno spremembo dolžine enojne sipalne poti . Tudi za ta parameter opazimo podobno odvisnost kot pri parametru za ostale lupine.

Končamo lahko s povprečnim številom kisikov, ki smo jih v modelno funkcijo dodali le za vzorca Co-2 in Co-3. Vzorec z manjšimi skupki ima ponovno prisotnih več kisikov. Ena izmed razlag, da smo v vzorcih Co-2 in Co-3 opazili prisotnost dodatne lupine kisikovih atomov je ta, da so kobaltovi atomi v stiku s kisikovimi atomi v silikatni mreži. V tem primeru obstaja možnost, da opazimo dodatno koordinatno lupino silicijevih atomov pri razdalji 3,3Å [32,33], ki so vezani na kobaltove preko kisikov.

Vzorec Co-kovina +O +Si 0,99(7) 0,9(2) 1,04(9) 1,06(9) Co-2 +O +Si 0,58(4) 0,50(9) 0,52(8) 0,49(8) Co-3 +O +Si 0,48(7) 0,3(5) 0,3(2) 0,3(2)

Vzorec [Å] [K] [eV] Co-kovina +O +Si 0,0069(4) 360(10) 0,008(2) 0,008(3) 5,4(6) Co-2 +O +Si 0,0077(4) 340(20) 0,006(2) 0,002(3) 4,4(7) Co-3 +O +Si 0,010(1) 300(70) 0,004(4) -0,01(1) 4(2)

Vzorec [Å] [Å] Co-kovina +O +Si 0,1(3) 1,98(4) 0,2(8) 3(4) 88 Co-2 +O +Si 0,6(3) 2,01(2) 1,3(4) 3,23(2) 130 Co-3 +O +Si 1,1(3) 2,01(2) 0,1(9) 3,3(9) 40

Tabela 9.6: Rezultati prilagajanja na področju prvih štirih vrhov in lupini kisikov ter lupini silicijev. Napaka na zadnji decimalki je podana zraven vrednosti v oklepajih. Spodnji dve tabeli sta nadaljevanje prve. Zgornja tabela vsebuje podatke o deležih sosedov v koordinatnih lupinah, srednja tabela vsebuje ostale podatke o kobaltovih lupinah, spodnja tabela pa vsebuje podatke o dodanih lupinah kisika in silicija ter o kvaliteti prilagajanja.

Za kovinski vzorec, ter vzorca skupkov Co-2 in Co-3 ponovimo prilagajanje podobno kot v prejšnjem primeru, le da sedaj v modelno funkcijo dodamo novo koordinatno lupino silicijev ter ustrezna variacijska parametra  in . Povprečni kvadrat odmika razdalje za silicij s smo fiksirali na 0,006Å2. Izkaže se namreč, da ne moremo hkrati zanesljivo določiti s in  saj je korelacija med njima prevelika. Za njegovo vrednost smo uporabili grobo oceno, ki upošteva, da je za bolj oddaljene sosede običajno večji kot za najbližje. Rezultati prilagajanja so navedeni v tabeli 9.6.

Odvisnosti, ki smo jih opisali na prejšnjih primerih, se ne spremenijo, zato jih ne navajamo ponovno. Osredotočimo se le na dodano silicijevo lupino. Preseneti nas ugotovitev, da je silicij prisoten le v vzorcu Co-2, v vzorcu Co-3 pa ga je zanemarljivo

malo. Upravičenost vpeljave nove koordinatne lupine silicijev lahko preverimo s primerjavo kriterija iz tabel 9.5 in 9.6. Ta se je z uvedbo nove lupine zmanjšal le pri vzorcu Co-2, kar pomeni, da je le pri tem vzorcu smiselno upoštevati lupino silicijev. V primeru kovine opazimo prisotnost silicija, čeprav vemo, da ga kovinski vzorec ne vsebuje. Podobno kot v primeru kisika, je dobljena vrednost 0,2 spodnja meja natančnosti s katero lahko določimo povprečno število silicijev v vzorcih s skupki.

Vsi trije vzorci se med seboj razlikujejo po prisotnosti ostalih elementov. Pri vzorcu Co-3 smo opazili le prisotnost kisika, silicija pa zanemarljivo malo. Iz tega lahko sklepamo, da je del atomov na površini skupka oksidiranih, v stiku s podlago pa je le majhen delež atomov, saj bi v nasprotnem primeru opazili več silicija. Pri vzorcu Co-2 smo poleg kisika opazili tudi znatno prisotnost silicijev. To lahko pojasnimo s tem, da imajo skupki velik stik s silikatno podlago, ki je sestavljena prav iz teh dveh elementov. Pri vzorcu Co-1 pa nismo opazili niti prisotnosti kisika niti prisotnosti silicija, torej ti vzorci niso oksidirani, delež atomov, ki so v stiku s podlago pa je zelo majhen, zato ne moremo opaziti njihovega prispevka v signalu velikega števila kobaltovih atomov, ki niso v stiku s podlago.

 

Analiza kristalne strukture skupkov

Z zadnjim prilagajanjem bomo preverili, ali lahko enolično prepoznamo kristalno strukturo skupkov. Doslej smo uspešno uporabili model fcc. Poskusimo modelirati strukturo skupkov še s kristalno strukturo hcp. Kot pri kovinskem Co modelno funkcijo sestavimo iz šestih ESP in 19 VSP, vse z dolžinami manjšimi od 5,2Å. V modelni funkciji ne upoštevamo dodatnih lupin kisikov in silicijev, saj je za preverjanje strukture najpomembnejše območje višjih koordinatnih lupin, ki se nahajajo pri večjih razdaljah. Opozoriti je treba na razliko med analizo kristalne strukture skupkov in analizo kristalne strukture kovine, ki smo jo izvedli v poglavju 9.1. Pri kovini smo lahko deleže sosedov v vseh koordinatnih lupinah fiksirali na, saj natančno poznamo kristalni strukturi hcp in fcc. V primeru skupkov pa ne poznamo deležev sosedov v koordinatnih lupinah, zato smo poleg ostalih parametrov variirali tudi deleže sosedov. Rezultati prilagajanja so v tabeli 9.7.

Čeprav bi lahko glede na kriterij rekli, da je model hcp dober vsaj v primerih Co-1 in Co-3, bi bila taka trditev prenagljena. Dobro ujemanje dobimo na račun deformacije modela hcp, saj so deleži sosedov v koordinatnih lupinah po prilagajanju modela signifikantno prerazporejeni. Pričakovali smo, da bo delež bolj oddaljene lupine manjši kot delež manj oddaljene lupine. Iz rezultatov prilagajanja pa vidimo, da je delež sosedov v tretji in šesti lupini očitno prevelik, delež sosedov v peti lupini pa izrazito majhen v primerjavi z ostalimi. Kljub relativno dobri kvaliteti prilagajanja lahko tako rečemo, da vsi naši vzorci vsebujejo skupke s kristalno strukturo fcc. V primeru vzorca Co-3 so deleži sosedov manj prerazporejeni, kar bi lahko pomenilo majhen delež skupkov v vzorcu s kristalno strukturo hcp. Tako ugotovitev lahko interpretiramo tako, da se pri majhnem številu atomov še ne more pokazati kristalna struktura. Atomi se v takem primeru lahko vežejo tudi na mesta, ki jih kristalna struktura ne predvideva. Večje število atomov pa se že uredi v kristalno strukturo.

Vzorec Co-1 0,68(8)   0,6(2) 1,2(3) 0,8(2) 0,3(9) 1,2(4) Co-2 0,63(6)   0,7(2) 1,1(3) 0,9(2) 0,3(9) 1,4(4) Co-3 0,55(9)   0,4(2) 0,8(3) 0,4(1) 0,1(9) 0,6(3)

Vzorec [Å] [K] [eV] Co-1 0,007(3) 0,017(8) 0,0072(8) 370(30) 5(1) 25 Co-2 0,001(2) 0,003(5) 0,0081(7) 320(30) 4(1) 320 Co-3 -0,005(9) -0,02(1) 0,011(2) 300(40) 1(2) 75

Tabela 9.7: Rezultati prilagajanja na področju prvih šestih vrhov v kristalni strukturi hcp. Napaka na zadnji decimalki je podana zraven vrednosti v oklepajih. Spodnja tabela je nadaljevanje prve. Zgornja tabela vsebuje podatke o deležih sosedov v koordinatnih lupinah, spodnja tabela pa vsebuje ostale podatke o kobaltovih lupinah.

 

 

 

E-mail:iztok.arcon@p-ng.si Last change: 13-Jun-2006