EXAFS

NANO SKUPKI

 

DOLOČANJE VELIKOSTI SKUPKOV Z METODO EXAFS

Velikost skupkov lahko posredno določimo z analizo podaljšane drobne strukture. Kot smo pokazali v prejšnjem poglavju, je amplituda posameznega sinusnega prispevka k podaljšani drobni strukturi sorazmerna s številom sosedov N v ustrezni koordinatni lupini okrog ioniziranega atoma. V primeru makroskopskega kristala kovine ima vsak atom v taki koordinatni lupini enako število sosedov z, v primeru skupka pa imajo atomi blizu površine manj sosedov, kot pa tisti v notranjosti. Če povprečimo število sosedov v koordinatni lupini čez vse atome v skupku, dobimo povprečno število sosedov na atom , ki je odvisno od razmerja med atomi blizu površine in vsemi atomi v skupku. Definirajmo še delež sosedov za vsako koordinatno lupino

(3.1)

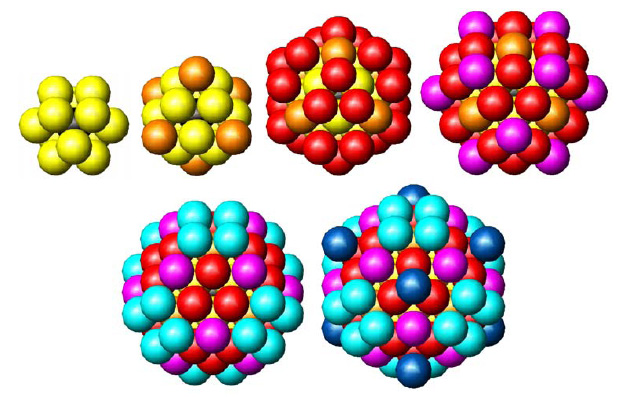
Slika 3.1: shematski prikaz krogelnosimetričnih kobaltovih skupkov s kristalno strukturo fcc (a=3.55Å). Premeri skupkov: 5.02Å, 7,10Å, 8,69Å, 10,04Å, 11,23Å, in 12,30Å. Skupek se veča z dodajankem plasti atomov okrog centralnega atoma. Vsaka plast je prikazan az drugo barvo.

Za izračun deleža sosedov za krogelnosimetrične skupke s kristalno strukturo fcc različnih velikosti sem sestavil računalniški algoritem, ki je najprej izračunal koordinate središč atomov, ki so od centralnega atoma oddaljeni manj kot izbrani polmer skupka.

Tako je na primer v kobaltovem skupku s polmerom 2,51Å okrog centralnega atoma le prva koordinatna lupina, v kateri je 12 atomov (slika 3.1). Z večanjem polmera postopoma dodajamo nove koordinatne lupine. Naslednja je pri razdalji 3,55Å, v kateri je 6 atomov. Sledi tretja ina s 24 ato četrta z 12 atomi pri razdalji 5,02Å itd. Našteti polmeri pomenijo razdaljo med središčema centralnega in njemu najbolj oddaljenega atoma, velikost samih atomov torej ni upoštevana. Algoritem nato prešteje sosede v prvih štirih koordinatnih lupinah okrog vsakega atoma v skupku ter izračuna povprečje čez vse atome v skupku. Deleži atomov v vsaki koordinatni lupini so izračunani po enačbi (3.1). Z večanjem skupka rastejo tudi deleži sosedov za vse štiri koordinatne lupine. Pri zelo velikih skupkih se vrednosti približujejo 1, torej rezultatu za kovino (slika 3.2).

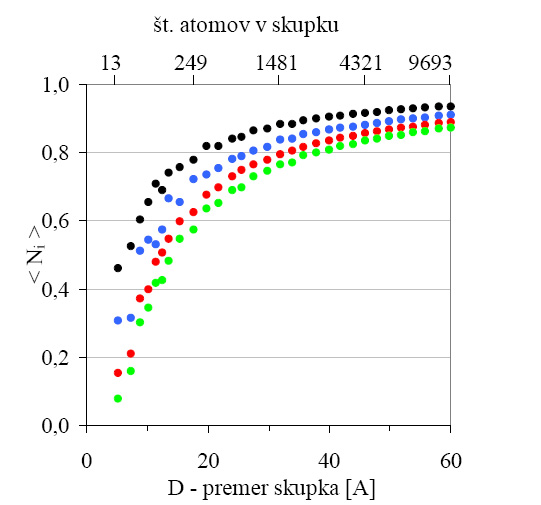
Slika3.2: Izračunani deleži sosedov za prvo koordinatno lupino (črno), drugo (modro), tretjo (rdeče) ter četrto (zeleno) v kobaltovih krogelnosimetričnih skupkih s fcc kristalno strukturo (=3.55Å) za različne premere skupka.

Najprej poskusimo razumeti, kako se spreminja delež sosedov za vsako koordinatno lupino s spreminjanjem velikosti skupka. Analitični model za krogelno simetrične skupke je predlagal M. Borowski [10].

V krogelnem skupku z premerom D je v vsaki koordinatni lupini pri razdalji r delež sosedov enak . Skupek orientiramo tako, da ima vsak atom v notranjosti skupka enega izmed sosedov v smeri z . Za začetek se omejimo le na te sosede, ker pa je skupek krogelnosimetričen, lahko sosede v ostalih smereh obravnavamo popolnoma enako. Krogelni model predpostavlja, da ima atom svojega soseda v smeri  prisotnega, če je sredina njune vezi oddaljena od površine skupka za manj kot r / 2 v smeri  (slika 3.3).

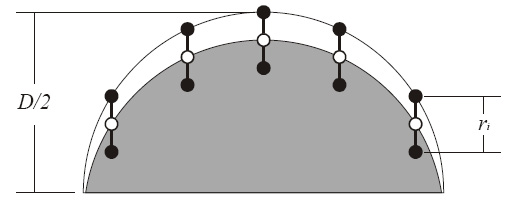
Slika 3.3: Shematski prikaz polovice prereza krogelnega skupka s premerom D. Atomi v skupku (črno) imajo svojega soseda v smeri prisotnega le, če je sredina vezi med dvema atomoma (belo) od površine skupka v smeri  oddaljena za r /2. To področje je označeno s sivo.

Delež atomov, ki imajo sosede v izbrani smeri  prisotne, je enak razmerju med volumnom sivo označenega skupka in volumnom celotnega skupka. Ker lahko na enak način obravnavamo sosede v poljubni smeri, je razmerje volumnov hkrati enako tudi deležu vseh sosedov v posamezni koordinatni lupini in se z velikostjo skupka spreminja kot [10]:

(3.2)

pod pogojem, da je. V nasprotnem primeru je delež sosedov enak nič.

Veljavnost modela lahko preizkusimo z numerično izračunanimi deleži sosedov za skupke različnih velikosti (slika 3.4). Model je dober za velike skupke s premerom večjim od 20Å, pri manjših pa pride do odstopanja med modelom in numeričnimi izračuni, ker so odstopanja od krogelne oblike že tako velika, da skupkov ne moremo več dobro aproksimirati s kroglo.

Natančnost pri določanju premera skupka je odvisna od natančnosti pri določanju deleža sosedov. Upoštevati moramo, da natančnost, s katero lahko pri EXAFS spektrometriji določimo delež sosedov, običajno ni boljša od ±0,03. Z analitičnim modelom lahko ocenimo, pri kateri velikosti lahko še določimo velikost skupka na 1Å natančno, če upoštevamo gornjo nenatančnost za delež sosedov. Zveza med nenatančnostjo deleža sosedov in napako velikosti skupka dD je:   

(3.3)

Iz enačbe lahko takoj opazimo, da je napaka velikosti skupka sorazmerna kvadratu velikosti skupka, saj je tipično r <<D. Dva krogelna skupka, ki se po premeru razlikujeta za 1Å, lahko na podlagi deleža prvih sosedov ločimo po velikosti samo, če je njun premer manjši od 11Å. Če velikost skupkov določamo iz deleža sosedov v nadaljnjih lupinah je metoda bolj občutljiva. S primerjanjem deležev sosedov iz četrte koordinatne lupine lahko z enako natančnostjo ločimo skupke s premerom do 15Å. Pri večjih skupkih postane ta metoda neobčutljiva. Na sliki 3.4 to opazimo po majhnem naklonu krivulje, ki predstavlja odvisnost deleža sosedov od velikosti skupka, nad omenjenimi velikostmi.

Pri majhnih velikostih skupkov, to je pod 15Å, analitični model ne opiše natančno numeričnih vrednosti, zato je ocena o natančnosti v tem področju le grob približek.

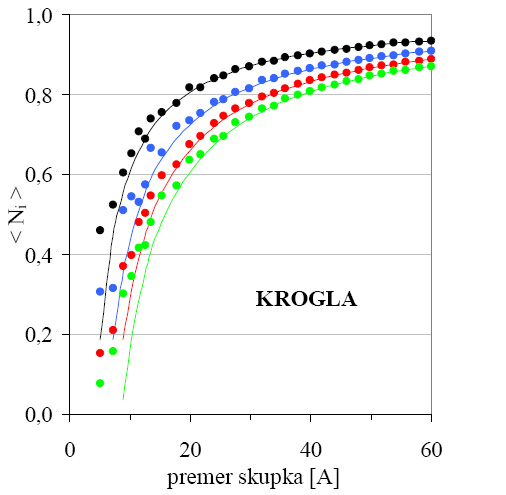
Slika 3.4: Primerjava analitičnega krogelnega modela (črte) z numerično izračunanimi vrednostmi (pike) za deleže sosedov v prvi (črno), drugi (modro), tretji (rdeče) ter četrti (zeleno) koordinatni lupini v kobaltovih krogelnosimetričnih skupkih s kristalno strukturo fcc (a=3,55Å) za različne velikosti skupka. Za velike skupke je model dober, pri majhnih pa pride do odstopanja od analitično izračunanih vrednosti.

 

POVEZAVA MED RELATIVNIMI DEGENERACIJAMI VSP IN ESP V SKUPKIH

V modelni funkciji (5.5) faktor Ni za enojne sipalne poti predstavlja povprečno število sosedov v ustrezni koordinatni lupini. Za sipalne poti, ki vključujejo več kot dva sipalca pa bi v splošnem morali upoštevati povprečno število sosedov v več koordinatnih lupinah. Namesto takega pristopa uporabimo v modelni funkciji povprečne degeneracije sipalnih poti . Te so v primeru ESP po vrednosti enake povprečnemu številu sosedov v izbrani koordinatni lupini. Za VSP vrednost povprečne degeneracije sipalnih poti ni več tako očitna, zato jo bomo poskušali povezati z vrednostmi za ESP. Da bi bila povezava za vse poti čimbolj enostavna uporabimo raje relativne degeneracije sipalnih poti , ki so povprečne degeneracije sipalnih poti, normirane z vrednostmi za kovino.

Za kristalno strukturo so degeneracije vseh sipalnih poti znane, v primeru skupkov pa jih ne poznamo. Če v skupkih povežemo relativne degeneracije večkratnih sipalnih poti z relativnimi degeneracijami enojnih sipalnih poti, se znebimo velikega števila prostih parametrov. Za prilagajanje nam tako ostane le majhno število variacijskih parametrov – relativne degeneracije enojnih poti.

Najpreprostejša je zveza med relativnimi degeneracijami enojnih poti ESPa in dvakratnih DSPa poti. Obe sta odvisni le od verjetnosti, da najdemo sosednji atom na njegovem pričakovanem mestu. Relativni degeneraciji obeh sipalnih poti sta tako v poljubnem skupku enaki, zato lahko zapišemo:                                   

(7.1)

Druga ugotovitev je ta, da je relativna degeneracija enaka za vse poti, ki vključujejo enako razporeditev atomov ne glede na položaj ioniziranega atoma. Verjetnost, da najdemo atome na pričakovanih mestih, je namreč neodvisna od izbire, na katerem atomu se sipalna pot prične. Relativne degeneracije poti iz linearne in trikotne družine lahko združimo v:       

(7.2)

(7.3)

Za naslednjo zvezo predpostavimo, da je skupek konveksen in da v notranjosti nima lukenj. Na podlagi te predpostavke lahko zaključimo, da je za linearna sipanja relativna degeneracija sipalne poti odvisna le od verjetnosti, da najdemo na pričakovanih mestih tista dva atoma, ki imata največjo medsebojno razdaljo izmed vseh atomov vključenih v sipalno pot. Tako lahko povežemo: 

(7.4)

Pri iskanju zveze med relativno degeneracijo trikotnih sipalnih poti  in relativnimi degeneracijami enojnih poti naletimo na težji problem. Vrednost za  mora biti v splošnem odvisna od treh parametrov: ,  in .

Za izračun  v krogelnem skupku sem uporabil postopek analogen postopku po katerem sem izpeljal analitični model za izračun deleža sosedov v valjastih in ploščatih skupkih. Namesto volumna preseka dveh teles tu potrebujemo volumen preseka treh teles, katerih središča so med seboj razmaknjena za vektorje ,  in . V primeru krogelnega skupka s polmerom R, so ta telesa krogle s polmerom R (slika 7.1).

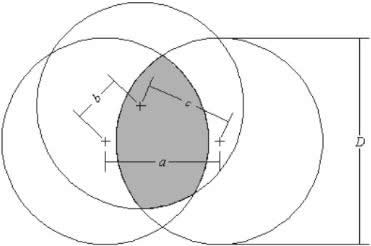
Slika 7.1: Shematski prikaz preseka (sivo) treh krogel s premerom D, katerih središča so med seboj razmaknjena za vektorje ,  in . Na sliki so središča pretirano razmaknjena zaradi boljše preglednosti. Razmerje med volumnom preseka in volumnom cele krogle je enako relativni degeneraciji sipalne poti TSPabc.

Tak model lahko preverimo na primeru linearne sipalne poti, kjer mora veljati tudi zveza (7.4). Presek treh krogel, katerih središča ležijo na isti premici z medsebojno oddaljenostjo a/2, mora biti enak preseku dveh krogel, katerih središči sta med seboj oddaljeni za (slika 7.2).

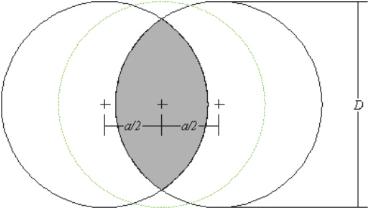
Slika 7.2: Shematski prikaz preseka (sivo) treh krogel s premerom D, katerih središča so med seboj razmaknjena za a/2. Na sliki so središča pretirano razmaknjena zaradi boljše preglednosti. Razmerje med volumnom preseka in volumnom cele krogle je enako relativni degeneraciji sipalne poti LSPa. Prisotnost sredinske krogle ne zmanjša volumna preseka.

Izračun preseka treh krogel za poljubne razmike njihovih središč je za naš namen prezapleten problem. Kljub temu pa lahko zaključimo, da je relativna degeneracija trikotnih sipalnih poti res enaka razmerju med volumnom preseka treh krogel in volumna cele krogle. S slik 7.1 in 7.2 lahko tudi vidimo, da ima največji vpliv na rezultat najdaljša stranica trikotne sipalne poti, zato lahko kot približek za  v krogelnosimetričnem skupku zapišemo podobno kot v enačbi (3.2) polinom tretje stopnje 

(7.5)

kjer je r najdaljša stranica trikotne sipalne poti, A, B in C pa so neznane konstante. V približku smo odstranili odvisnost od ostalih dveh stranic trikotne sipalne poti. Približek je zelo natančen za sipalne poti, ki imajo eno stranico izrazito daljšo od ostalih, ter manj natančen za sipalne poti z obliko enakostraničnega trikotnika. Konstante bi lahko določili z metodo najmanjših kvadratov na numerično izračunanih vrednostih, vendar nas za praktično uporabo zanima le zveza med  in . S primerjavo enačb (3.2) in (7.5) lahko zapišemo približno zvezo         

(7.6)

kjer je X konstanta linearnega popravka in kjer smo zanemarili popravke v kvadratnem in kubičnem členu. Konstanto X lahko določimo na numerično izračunanih vrednostih za vsako sipalno pot posebej. Zavedati se moramo, da je enačba (7.6) matematično gledano zelo grob približek, vendar vseeno zadostuje za potrebe modeliranja signala EXAFS (slika 7.3), saj znašajo signali trikotnih poti le nekaj procentov celotne podaljšane drobne strukture.

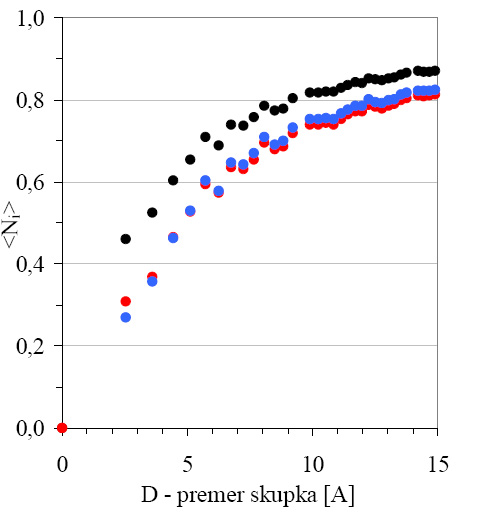
Slika 7.3: Primerjava numerično izračunanih  (modro) s tistimi, ki jih napove model (rdeče). Za primerjavo so na grafu tudi vrednosti za  (črno). Primerjava je bila narejena na različno velikih krogelnih skupkih s kristalno strukturo fcc, =3,55. Konstanta linearnega popravka za TSP111 je v tem primeru 1,358.

Za obliko palčke lahko enačbo (7.5) zapišemo kot polinom druge stopnje, za obliko ploščice pa kot polinom prve stopnje. Zveza med  in  pa v splošnem ostane enaka, le z različno konstanto X. Ker v primeru ploščice ne zanemarimo kvadratnega in kubičnega člena, je enačba (7.6) za ugotovljene X v resnici popolnoma točna.

Vrednosti za konstante linearnega popravka dobimo če z metodo najmanjših kvadratov minimiziramo funkcijo   

(7.8)

Dobljene vrednosti za vse trikotne poti in za vse osnovne oblike skupka so zbrane v tabeli 7.1. Izkaže se, da lahko v praksi za konstanto linearnega popravka uporabimo povprečno vrednosti vseh treh oblik X.

Z enačbami (7.1, 7.4 in 7.6) smo povezali relativne degeneracije VSP z normiranimi degeneracijami ESP in s tem občutno zmanjšali število variacijskih parametrov prilagajanja.

sipalna pot	X (krogla)	X (palčka)	X (ploščica)	Xpovp
TSP111	1,357(8)	1,408(6)	1,500	1,42
TSP112	1,05(5)	1,08(4)	1,000	1,04
TSP113	1,01(1)	1,02(2)	1,000	1,01
TSP123	1,08(2)	1,13(3)	1,250	1,15
TSP133	1,13(3)	1,209(8)	1,250	1,20
TSP134	1,073(8)	1,19(6)	1,250	1,17

Tabela 7.1: Vrednosti za konstanto linearnega popravka za vse uporabljene trikotne poti in za vse tri osnovne oblike skupka. V zadnjem stolpcu so povprečne vrednosti za vsako trikotno pot. Ocenjene napake na zadnjo decimalko so pripisane v oklepaju. Za ploščico so vrednosti točne.

 

 

,                        

E-mail:iztok.arcon@p-ng.si Last change: 20-Apr-2006