 |
 |
||||||||||
Discussion and results
The
deep MPE from the 1s3d group on can be well described by relatively
simple model combinations of a resonant, a shake-up and a shake-off
term. As shown in Table 4, pairs of terms are often included to
model multiplets with a large and pronounced splitting. The model
parameters,
collected in Table 4, are obtained by a least square fit using
the nonlinear Levenberg-Marquardt algorithm. The procedure, however,
is not entirely straightforward, due to the large number (~25)
of
parameters and possible correlations among some of them. To avoid
local minima in the variational functional, corresponding to unphysical
solutions, the algorithm is applied sequentially. In the initial
steps, the relative energies and widths of the ansatz terms are
kept fixed at their theoretical values and only the amplitudes are
varied,
so that a linear problem with a well defined single minimum is
solved. In this way, the completeness of the ansatz is tested. The
residual
of the data, after subtracting the model, may show the presence
of additional channels, as in the case of the 1s3d group. In the
final
steps, the widths and energy parameters are freed to vary one by
one, to test their stability. The rationale of letting the widths
vary is the fact that the model components describe a whole multiplet
whereby their width can be increased over the lifetime value. The
range of shake-off components is fixed at the 40 % of the relative
threshold energy as already mentioned.
Similarly, the restriction of energy parameters to their HF or DF values
may be removed at the final stage of the analysis to allow for small
adjustments since the effective centroids of the model components need
not coincide with the DF multiplet averages. The 1s3s group, however,
is treated more simply: the singlet-triplet splitting of ~6 eV is ignored
in the model since the small signal-to-noise ratio makes only the separation
of shake-up and shake-off statistically significant.
The agreement of the model energies with theoretical values depends
on the relative energy of the coexcitation: the difference amounts
to a few tenths of eV in valence coexcitations of Table
1, and less
than 2 eV in the deep MPE of Table 4. The 5 eV difference of the 1s3s
group has additional causes in the well-known weak convergence of HF
calculation for configurations with more than one open s subshell (three
in 1s3s Rb!), and in the simple two-component model. It should be noted,
however, that the accuracy of the energy parameter can directly be
estimated only in the 1s3d group with a recognizable resonant component.
In 1s3p and 1s3s groups with a predominant edge shape, the energy parameter
of the model edge is not so sharply defined. The same apparent edge
can be described with a model edge with an arbitrary shift upwards
of the order of its width, if a resonance of an appropriate amplitude
is inserted. In the same way, the threshold of a model shake-off component
is correlated with the amplitude of the preceding model edge. In both
cases, a meaningful value of amplitude is only obtained when the correlation
is removed by fixing the relative energy at the theoretical value.
In this view, the parameters in the Table 4 represent minimal models
sufficient to describe the MPE groups within experimental accuracy.
Or, in different words, we show that the MPE features can be explained
as simple combinations of well-known channels. The relevant results
of the analysis are the best-fit amplitudes of the components; the
energy and width parameters show the concordance with theoretical predictions.
The estimated error of the amplitudes is one or two units of the last
digit.
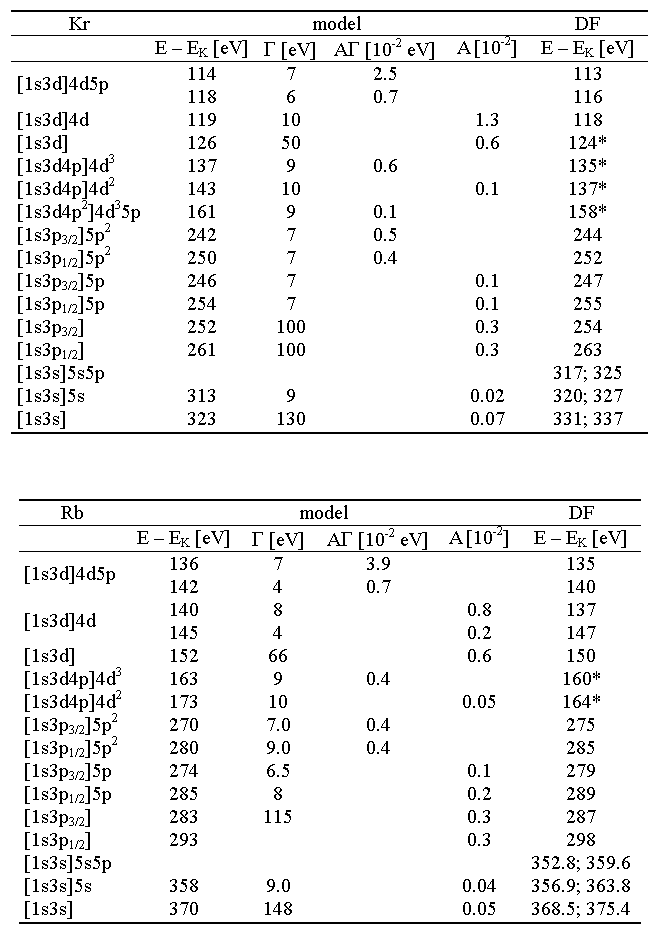
Table
4. Model parameters of the Kr and Rb 1s3d, 1s3p
and 1s3s groups: (threshold) energies, widths/ranges and resonant
intensities or shake amplitudes together with calculated energies
(DF multiplet centers) of the corresponding electron transitions.
Double values for the 1s3s group denote singlet-triplet splitting
where a single model component is used. The estimated error
of the amplitude parameters is 1 or 2 units of the last digit:
the accuracy of the data in general is discussed in Chapter
4. *HF value |
 |
The model amplitudes in Table 4 invite comparison with earlier
Kr data. Among recent reports only Schaphorst et al [8] and
Pade¾nik Gomil¹ek
et al [26] include cross sections of separate channels. The latter
use a similar approach to ours and report the 1s3d and 1s3p shake-up
amplitudes as 1.4% and 0.3 %, respectively, agreeing with our data
to within experimental error. Schaphorst composed the models of
MPE features from ab initio calculated cross sections and demonstrated
their fit with the experimental spectrum. His values of 1.4 % and
0.2
% for 1s3d and 1s3p shake-up, respectively, agree well with our
results. The value 3.7 % for the 1s3d shake-off, however, is
six times larger
than ours. The fit of this calculated value with experimental data
is only possible with an arbitrary choice of the baseline onto
which the 1s3d feature is superposed. Since the curvature of
the baseline
is particularly large in this region, we feel that our exponential
ansatz, taking into account the entire MPE region, produces a more
reliable value for the shake-off amplitude. The 1s3p shake-off
amplitude of 0.8 % is again close to our value, conceivably
due to the smaller
curvature of the baseline beneath the 1s3p group.
There are no earlier data on atomic Rb absorption for comparison,
but the presence of MPE in EXAFS spectra of Rb+ ion in a solution
has been
demonstrated [48]. Recently, however, De Panfilis et al [49] have
reported a measurement on molten Rb droplets: the spectrum shows
all of the
major MPE groups with a negligible contribution of the structural
signal. The decomposition into principal excitation channels is
indicated but
no quantitative data are extracted.
In the present analysis the investigated spectral region has been
wide enough, comprising several separate MPE groups, to attract
attention
to the increased slope above the edge and to show that its segments
seen in the spaces between MPE groups resemble a single continuum.
With a simple heuristic ansatz the entire spectrum is transformed
into a more comprehensible form. We do not claim that the physics
of virtual
Auger excitations and PCI contribution is adequately represented:
indeed, it is rather evident that the ansatz needs some local adaptation.
The
removal of a single exponential cannot flatten out all gaps between
subshell groups: a larger decay constant would be needed for the
region of 5s, 4p and 4s coexcitation groups, and a smaller one
for the deep
coexcitation. Evidence for some interference between this channel
and the 3d coexcitation is given by the strong curvature of the
cross section
just below the 1s3d edge which escapes modeling with the standard
ansatz. Nevertheless, the single exponential successfully removes
the anomalous
slope over the entire MPE region and over an order of magnitude.
A considerably more precise measurement will be necessary to improve
the ansatz with reliable additional terms.
The
Rb vapor absorption experiment has provided the first instance of
a comprehensive MPE spectrum outside the noble-gas group and has
opened the way to comparison of MPE between neighbors. The advantage
is twofold: the alkali spectra are less transparent due to the
richer multiplet structure, so that the identification of features
is considerably
facilitated by the simpler structure of spectra of their noble-gas
predecessors. On the other side, the explanation of some ambiguous
reaction channels in noble-gas spectra is aided by the evolution
of the excitation scheme in the Z+1 case.
The deconvolution of natural width in Kr and Rb has considerably improved
the explanation of the edge region and of the strong valence MPE where
the signal-to-noise ratio is still sufficiently high so that some expansion
of noise can be tolerated in sharpening of the spectral features.
Together with the sharper view of the MPE features the PCI contribution
is fully recognized in its span over the entire MPE region. A heuristic
model is proposed in the absence of theoretical data. With the model,
the photoabsorption cross section is reasonably transformed into a
superposition of contributions of consecutive shake channels.
The unifying principle of the MPE spectra in both elements is the ground
state CI: the admixture of the [4p^2]4d^2 configuration introduces
strong additional channels in the three most prominent groups of MPE.
The
difference between the two elements is less striking: it is epitomized
by 5s coexcitations in the Rb edge region and by the specifically
strong 5s-5p coupling. Another instance is the imminent 4d collapse.
In many
of these aspects, the Kr-Rb pair behaves in complete analogy with
the Ar-K homologues. It is thus possible to introduce the concept of
a
noble-gas and/or alkaline MPE scheme.
Acknowledgement: Support of Slovenian Ministry of Education, Science and Sport, and Internationales Büro des BMBF (Germany) is acknowledged. The experiment at the ESRF was performed under proposal No He-375; expert advice on BM29 beamline operation by A.Filipponi and M. Borowski is gratefully acknowledged, as well as the assistance of the former in the deconvolution procedures.
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
E-mail:iztok.arcon@p-ng.si Last change: 28-Jun-2006 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||