 |
 |
||||||||||
Clusters shape and morfology
Related
publications:
1) I. Arčon, A. Tuel, A. Kodre, G. Martin, A. Barbier, J. Synchrotron Rad., 8,
(2001), p. 575-577 (reprint)
2) A. Barbier, A.Tuel, I. Arčon, A. Kodre, G. Antonin Martin, Journal
of Catalysis Vol. 200 (2001) 106-116
We have shown that different routes of preparation of the metallic cobalt dispersed
on microporous silica lead to formation of fcc Co clusters of different average
sizes. Assuming a spherical shape of the clusters, the samples Co/SiO2-1,
Co/SiO2-2 and Co/SiO2-3 contain clusters with average diameters of 13.5 A,
10.2 A, and 7.2 A, respectively.
 |
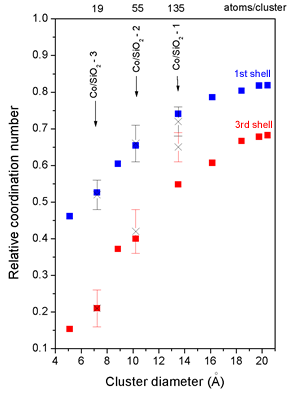 |
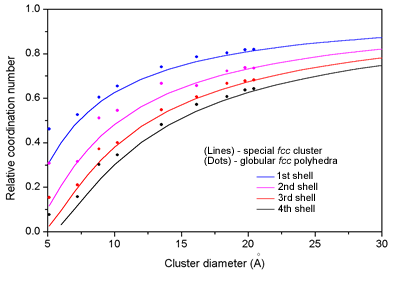
| Fig. 1. Relative coordination number in the first four neighbor shells as a function of cluster diameter. Left: (dots) - globular fcc polyhedra, (line) - spherical fcc clusters. Right: (sqare) - model globular fcc polyhedra, (cross) - experimental values for the three cluster samples. | |
The average sizes of the clusters, deduced from the observed reduction
of the average number of neighbours are significantly smaller
than those obtained by
magnetic measurements or TEM. Such observations on catalytic samples have
been reported previously by different authors [Dalmon
et al., 1983, Shido et al.,
1998]. An explanation of the discrepancy, besides the one cited earlier [Shido
et al., 1998] which employs specific models of disorder at the cluster surface,
can be given by an aggregate morphology of Co particles.
It should be emphasized that the directly determined experimental
parameter in EXAFS analysis is the average number of neighbors.
It is correlated linearly
to the fraction of surface atoms in a cluster, as can easily be shown for
large
clusters: atoms in the inside contribute the full coordination number of
neighbors (12 in fcc lattice), and those at the surface contribute a deficient
number (9
in fcc). Thus, the average number of (first) neighbors is a direct measure
of the specific surface of the dispersed metal, and (should be) a direct
measure
of the catalytic activity. The conclusion is largely independent of the
cluster shape and size distribution. - The value of the cluster
diameter, on the
other side, depends critically on the assumptions of uniformity and globular
shape.
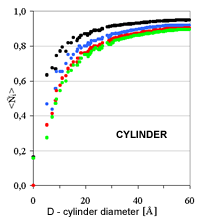
In the other two cases of simple shapes, cylindrical rods and platelets,
the extracted size parameter (diameter of rods and thickness of the platelets)
would
differ for a small numerical factor (2/3 in fcc). However, it would invariably
be the small shape parameter. The average number of neighbors is largely
insensitive to the large size parameter, i.e. the length of the rods or
the width of the
platelets. The conclusion can be extended to aggregates of the simple shapes
(dendrites of globules, rods or platelets) as long as the attachment area
is small. )
 |
 |
 |
 |
 |
 |
||
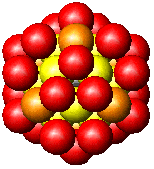
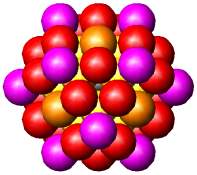
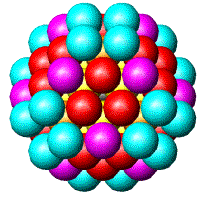
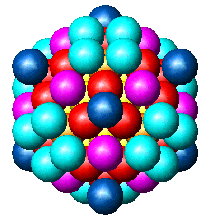
| Fig. 2. Globular fcc metalic clusters with increasing number of atoms and a corresponding increase in cluster diameter. Colors indicate consecutive shells of atoms. | |||
If globular clusters with perfect fcc structure are formed, as
assumed (in the EXAFS model, then EXAFS is shown to give reliable
estimate of the
average
particle
size [Borowski, 1997; Frenkel, 1999; Montano et al. 1986]. Larger aggregates
are composed of small globular Co crystallites, attached to each other
only by a small fraction of their surface, giving the large overall diameter
in
MM measurements.
For example, samples Co/SiO2-3 and Co/SiO2-2 prepared in ammonia possess
aggregates with diameters of ca. 44 A and 92 A, respectively, while the
corresponding globule
sizes are 7.2 and 10.2 A.
Tight aggregates are also possible, whereby the small globular clusters
assume the role of domains in polycrystalline materials. The EXAFS estimate
of the
size refers to the region of short-range order within the domain. A similar
model
has been previously proposed for Ni/SiO2 catalysts [Dalmon
et al., 1983] and MoS2 on oxidic or carbon carriers [Shido
et al., 1998]. There is
no direct relationship
between the size of the domains and those of the large cobalt particles.
It is also not clear however what mechanism would produce that particular
morphology.
 |
 |
 |
|
| Fig. 3. Characteristic geometrical shapes of nanoclusters | |
 |
 |
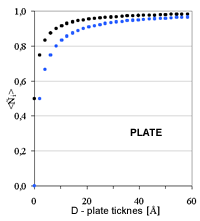 |
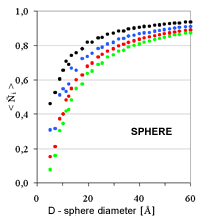
| Fig. 4. Relative coordination number in the first four coordination shells as a function of cluster diameter for three characteristic cluster shapes: sphere, cylinder, plate | ||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
E-mail:iztok.arcon@p-ng.si Last change: 02-Jun-2006 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||